|

Тем временем уже стала разрабатываться новая теория портфеля (МРТ). Марковиц (Markwitz, 1952) определил меру как дисперсию распределения возможных прибылей риска портфеля. Формально дисперсия совокупности определяется cледующей формулой:
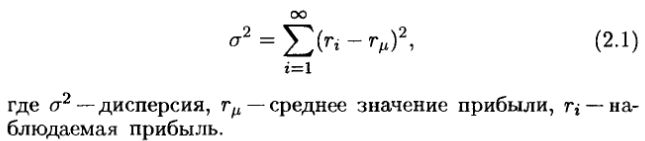
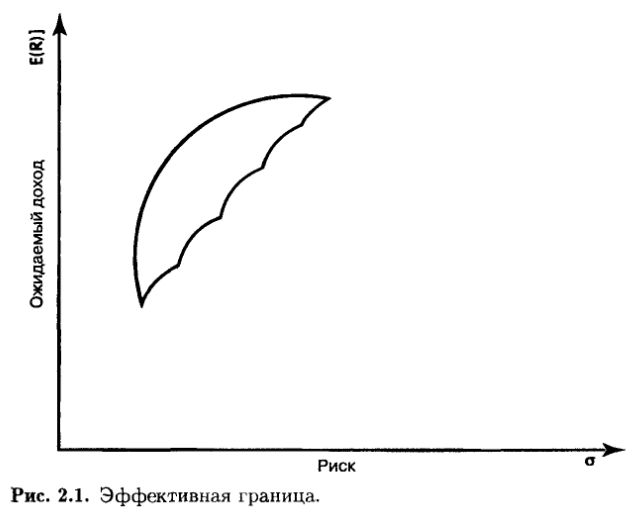
В пределе дисперсия должна измерять рассеяние возможных прибылей относительно среднего значения прибыли. Квадратный корень из дисперсии, или стандартное отклонение, измеряет вероятную величину отклонения прибыли от своего среднего значения. Если мы используем концепцию ожидаемой прибыли Осборна, мы сможем оценить вероятность отклонения реальной прибыли от среднего. Чем шире рассеяние, тем больше будет стандартное отклонение, и тем рискованнее капитал. Само по себе использование дисперсии требует того, чтобы прибыли были нормально распределены. Однако, если фондовые прибыли следуют случайному блужданию, и случайные переменные являются независимыми идентично распределенными (IID), то тогда по утверждению центральной предельной теоремы (или закону больших чисел) распределение должно быть нормальным и дисперсия – конечной. Инвесторы, таким образом, должны располагать портфелем с наивысшей ожидаемой прибылью для определенного уровня риска. Инвесторы предполагаются не склонными к риску. Этот подход стал известен как «эффективность по среднему/дисперсии». Кривая, представленная на рис. 2.1, была названа «эффективной границей», поскольку эта замкнутая линия заключает внутри себя портфели с наивысшими уровнями ожидаемых доходов для данных уровней риска, или стандартного отклонения. Инвесторы должны предпочитать эти оптимальные портфели, основанные на модели рационального инвестора.
Эти концепции были расширены Шарпом (Sharpe, 1964), Литнером (Litner, 1965) и Моссином (Mossin, 1966) и вылились в известную модель оценки капитальных активов (САРМ), – это название было придумано Шарпом. САРМ объединила гипотезу эффективного рынка (ЕМН) и математическую модель теории портфеля Марковица в модели инвесторского поведения, основанной на рациональных ожиданиях в рамках общей концепции равновесия. В частности, она предполагает, что инвесторы имеют однородные ожидания, касающиеся прибыли. Следовательно, они одинаковым образом интерпретируют информацию. САРМ была выдающимся достижением трех независимых исследователей.
Ввиду того что САРМ широко обсуждалась в литературе, наше рассмотрение здесь будет ограничено в основном аспектами, которые соотносятся с предпосылкой о том, что необходима новая парадигма. САРМ начинается с предположения, что мы живем в мире, свободном от издержек на совершение сделок, комиссионных и налогов. Эти упрощающие предположения были необходимы для отделения инвесторского поведения от ограничений, накладываемых обществом. Физики часто поступают подобным образом, например, предполагая отсутствующим трение. Далее САРМ говорит, что каждый может заимствовать средства и давать взаймы на безрисковой ставке процента, которая понимается обычно как 90-дневная казначейская ставка. В итоге это предполагает, что все инвесторы стремятся к средне-дисперсной эффективности Марковица, Т. е. желают иметь портфель с наивысшим уровнем ожидаемой прибыли для заданного уровня риска и в целом не любят рисковать. Риск снова определен как стандартное отклонение прибыли. Инвесторы, таким образом, рациональны в смысле Осборна и Марковица.
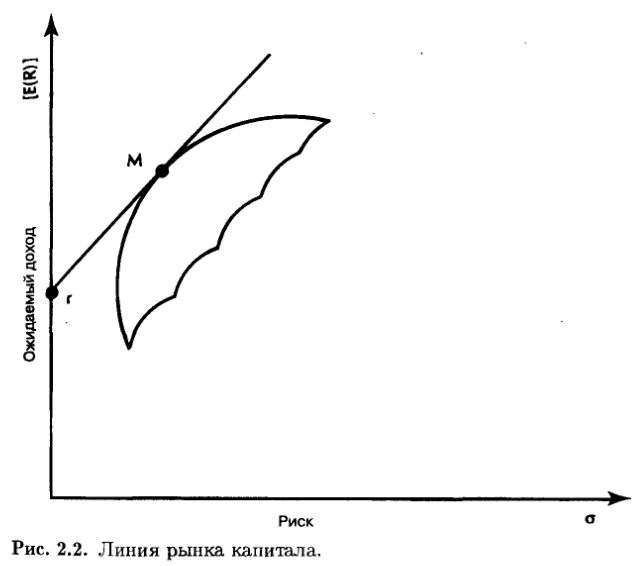
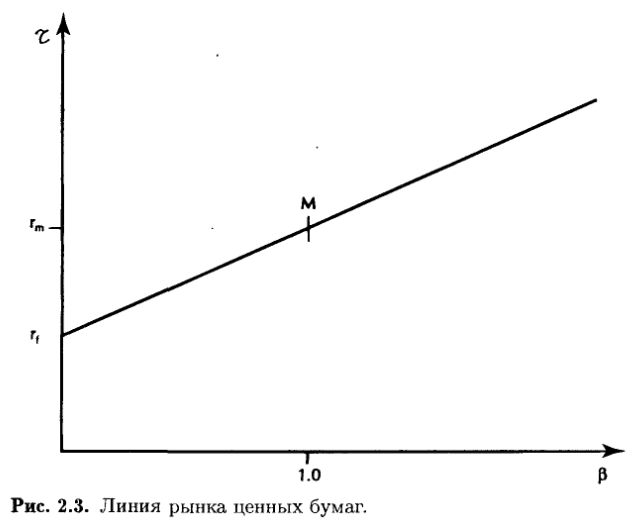
Основываясь на этих предположениях, САРМ продолжает делать заключения о поведении инвесторов. Во-первых, оптимальным портфелем для всех инвесторов должна быть некоторая комбинация рыночного портфеля (все рисковые активы капитализационно взвешены) и безрисковых активов. Этот тип портфеля показан на рис. 2.2. Линия рынка капитала касается эффективной границы рыночного портфеля (М), и точка ее пересечения с осью Y есть безрисковая ставка процента (r). Уровень риска можно менять путем добавления безрисковых активов, чтобы уменьшить стандартное отклонение портфеля, или путем получения кредитов по этой ставке, чтобы заемными средствами воздействовать на рыночный портфель. Портфели, которые лежат на этой прямой, называются лежащими на линии рынка капитала (CML – Capital Market Line) и они количественно преобладают над портфелями, лежащими на эффективной границе, – инвесторы предпочитают такие портфели всем другим. Добавим, что инвесторы не компенсируют убытков от нерыночного риска, поскольку оптимальные портфели лежат на CML. Эта модель также утверждает, что активы с более высоким риском должны иметь более высокие прибыли. Так как риск теперь отнесен к рыночному портфелю, используется линейная мера чувствительности риска ценной бумаги к рыночному риску. Эта линейная мера носит название бета. Если все рисковые активы разместить в координатах «бета – ожидаемая прибыль», результатом будет прямая линия, пересекающая ось У на безрисковой ставке процента и проходящая через рыночный портфель. Она называется линией рынка ценных бумаг (SML – Security Market Line). Ее график показан на рис. 2.3.
Это короткое и по необходимости неполное обсуждение САРМ призвано показать сущностную зависимость модели от стандартного отклонения как меры риcка. По смыслу САРМ требует эффективного рынка и нормального или логнормального распределения прибыли, поскольку дисперсия предполагается конечной. Предлагая практические количественные методы, САРМ остается стандартом для любой новой модели инвесторского поведения. Теория портфеля Марковица объяснила, почему диверсификация уменьшает риск. САРМ объяснила, каким образом должны были бы вести себя инвесторы, если они рациональны. Практики вынуждены были согласиться, что предположения, лежащие в основе САРМ, хотя и являются упрощающими существо дела, тем не менее не умаляют полезности модели. ЕМН стала широко применяться в качестве логического обоснования для использования гауссовского логнормального распределения прибыли. Борьба за признание модели, возможно, заставила этих ранних поборников количественных методов настаивать на том, что ЕМН является истиной. Объединение ЕМН и САРМ и ее модификаций стало общеизвестно как новая теория портфеля (МРТ – Modern Portfolio Theory). Все та же борьба за признание, вероятно, стала причиной того, что обсуждение нежелательных подробностей было отодвинуто на задний план.
ЕМН подкрепила МРТ, и дисперсия, и стандартное отклонение были приняты сообществом инвесторов как истинные меры риска. Повторим снова, ранние основатели теории рынков капитала были хорошо осведомлены об этих предположениях и их ограниченности. Самуэльсон, Шарп и Фаме (среди других) опубликовали работы, модифицирующие МРТ для не нормальных распределений. Эмпирические данные 60-х годов из статьи Мандельброта (1964) свидетельствовали в пользу устойчивого распределения Парето; в этой статье он показал, что поскольку прибыли не нормально распределены, имеется необходимость для возможной ревизии ЕМН и МРТ. (Мы рассмотрим устойчивое распределение Парето в деталях в части 2, где будем знакомиться с фракталами.) Было уже накоплено много фактов, свидетельствующих о том, что прибыли не следуют нормальному распределению, в то время когда Шарп (Sharpe, 1970) и Фамэ и Миллер (Fame, Miller, 1972) опубликовали свои работы; обе книги содержат разделы, в которых говорится о необходимости модификации стандартной теории портфеля с учетом устойчивого распределения Парето.
В 1970-х годах эта дискуссия утихла, если не считать отдельных академических статей, среди которых выделяется работа Ролла (Roll. 1977). Развитие экономики финансов продолжалось на основе слабой формы ЕМН и ее предположении о том, что ценовые изменения независимы. Вдобавок, нормальное распределение с его гауссовским предположением о независимости стало общепринятым в моделировании. Применения эконометрики к рынкам капитала стали более комплексными, так как ЕМН получила широкое признание и все меньше ставилась под вопрос. Главными достижениями были модель расчета цен опционов Блэка и Шоулса (Black, Scholes, 1973) и арбитражная ценовая теория (APT – Arbitrage Pricing Theory) Росса (Ross, 1976). APT является более общей ценовой моделью, чем САРМ; она предполагает, что ценовые изменения происходят в результате неожиданного изменения факторов и, следовательно, может манипулировать с нелинейными отношениями. Однако практически для инструментального оснащения APT была использована стандартная эконометрика (включая предположение о конечной дисперсии). APT стала альтернативной теоретической ценовой моделью, которая не зависела от квадратических функций полезности.
В последние годы теоретические модели стали появляться реже. Работы 1980-х годов были сосредоточены на эмпирических исследованиях и приложениях уже существующих моделей. Единственное теоретическое достижение, получившее широкое признание в последние годы, постулировало, что рыночная волатильность изменяется во времени. Это означает, что волатильность зависима от своих предыдущих уровней. Эта модель вела свое происхождение от авторегрессионных условных гетероскедастических (ARCH) моделей Ингла (Engle, 1982). От его оригинальной работы берут свое начало многие разновидности моделей, основанных на ARCH. Однако все они исходят из предположения о кратковременной памяти в исследуемых процессах, а также – в той или форме – о рыночной эффективности.
|