|

Развитие фрактальной геометрии стало одним из самых полезных и прекрасных открытий в математике. С помощью фракталов математики создали систему, которая описывает природные формы, используя небольшое количество терминов и правил. Сложность рождается из простоты. Фракталы придают сложности структуру и красоту – хаосу. Нас интересует, каким образом фракталы возникают в нелинейной динамике. Большинство природных форм и временных рядов наилучшим образом описываются фракталами. Естественно заключить, что нелинейность и фракталы являют собой геометрию хаоса.
Взгляд на мир под углом зрения фрактальной геометрии сильно отличается от того, который предлагает нам геометрия евклидова. Евклидова геометрия, изучаемая нами в школе, есть выражение и развитие древнегреческой философии.
Античные греки ответственны за привнесение причинности в западную культуру. Наблюдая вокруг себя жизнь, полную кажущихся хаотическими случайных событий, они искали чистые формы и порядок, спрятанные под покровом повседневного шума. Они хотели свести природу к этим простым формам. Их инструментом была математика. Многое из написанного древними греками исполнено мистического родства с математикой. Во многих отношениях наша потребность найти структуру в природе есть наследие античности. Существует много параллелей между тем взглядом, который ищет чистых форм в основе каждодневной жизни, и поисками экономистов циклического порядка в шуме ежедневных сделок, о котором рассказано в гл. 3. Античные греки верили в порядок чисел и его родство с порядком универсума. Они работали над тем, чтобы интегрировать числа в природу посредством системы естественных законов.
Евклид собрал воедино отдельные законы, открытые Пифагором, Аристотелем и другими, и создал из них цельную систему. Его базовая структура (аксиомы, теоремы и доказательства), которая легла в основу плоской геометрии, широко используется поныне. Техника и землепользование тесно связаны с этими античными законами.
Евклид свел природу к чистым и симметричным объектам: точка, одномерная линия, двумерная плоскость, трехмерное тело. Среди тел имеется ряд чисто симметричных форм, таких, как сферы, конусы, цилиндры, блоки. Ни один из этих объектов не имеет в себе отверстий и внешних неровностей. У каждого правильная гладкая форма. Для греков симметрия и сплошность были признаками совершенства. Только совершенство предполагалось в природе.
В реальности природа отвергает симметрию, так же как она не любит равновесия – эти в некотором смысле эквивалентные состояния. Природные объекты огрубленных форм не являются разновидностями чистых евклидовых структур. В результате создание компьютерных изображений гор при помощи евклидовой геометрии представляет собой устрашающую задачу, которая требует множества строк программного кода и большого количества обращений к датчику случайных чисел. С помощью же фрактальной геометрии гора может быть создана на экране дисплея посредством всего лишь нескольких повторно применяемых правил.
Бенуа Мандельброт может быть назван Евклидом фрактальной геометрии. Он собрал наблюдения математиков, которые изучали «монстров», т. е. объекты, не определимые на путях евклидовой геометрии. В итоге обобщения этих математических работ и своего собственного озарения он создал геометрию природы, которая преуспела в описаниях асимметричности и невнятных форм. Мандельброт сказал: «горы не являются конусами, и облака – не сферы».
Наверное, неспособность евклидовой геометрии описывать природные объекты лучше всего демонстрирует следующее свойство. В евклидовой геометрии чем больше мы приближаем свой взгляд к объекту, тем проще он становится. Трехмерный блок становится двумерной плоскостью, затем одномерной линией, до тех пор пока не станет точкой. С другой стороны, природный объект являет нам все больше и больше деталей по мере того, как мы приближаем взгляд – на всем пути, вплоть до субатомного уровня. Этим свойством обладают фракталы. Чем пристальнее мы их изучаем, тем больше деталей можем увидеть.
Так что же такое фрактал? Всеобъемлющего, окончательного определения фракталов не существует. Мандельброт (1982) первоначально определил фракталы, основываясь на топологической размерности. Впоследствии он отказался от этого определения. Мы будем пользоваться следующим рабочим определением: фрактал есть некоторая самосоотнесенность, или самоподобие. Один из самых наглядных естественных фракталов – это дерево. Древесные ветви следуют фрактальному скейлингу. Каждое ответвление со своими собственными ветвями подобно всему дереву целиком в качественном смысле.
Фрактальные формы обнаруживают пространственное самоподобие. Фрактальные временные ряды имеют статистическое самоподобие во времени. Они являются случайными фракталами и имеют больше общего с естественными объектами, чем чистые математические фракталы, которые будут нами рассмотрены в первую очередь. Мы будем изучать в основном фрактальные временные ряды, но фрактальные формы дают хорошую основу для интуитивного постижения, поскольку для них «самоподобие» имеет наглядный смысл. По аналогии с ними легче будет понять фрактальные временные ряды. Чтобы пробудить читательский интерес, лучше думать о временном ряде рыночной прибыли.
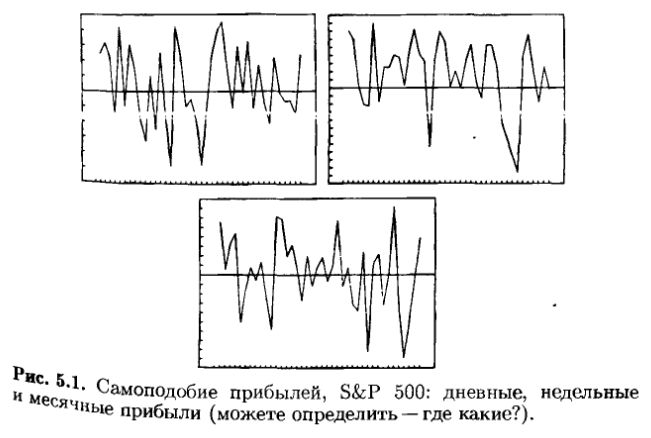
На рис. 5.1 показаны дневная, недельная и месячная прибыли по статистике S&Р 500 для сорока последовательных наблюдений. Можно ли определить, какой из графиков перед нами, не зная масштабов измерений по осям х и у? Таким образом, рис. 5.1 иллюстрирует самоподобие фрактального временного ряда.
|