Фрактальные формы

Фрактальные формы могут порождаться многими путями. Простейший из них – задать порождающее правило и выполнить последовательность итераций. На рис. 5.2 показан пример. Мы начинаем со сплошного равностороннего треугольника (рис. 5.2а). Затем удаляем равносторонний треугольник из первоначальной фигуры – остается три меньших сплошных треугольника и пустой треугольник в середине (рис. 5.26).

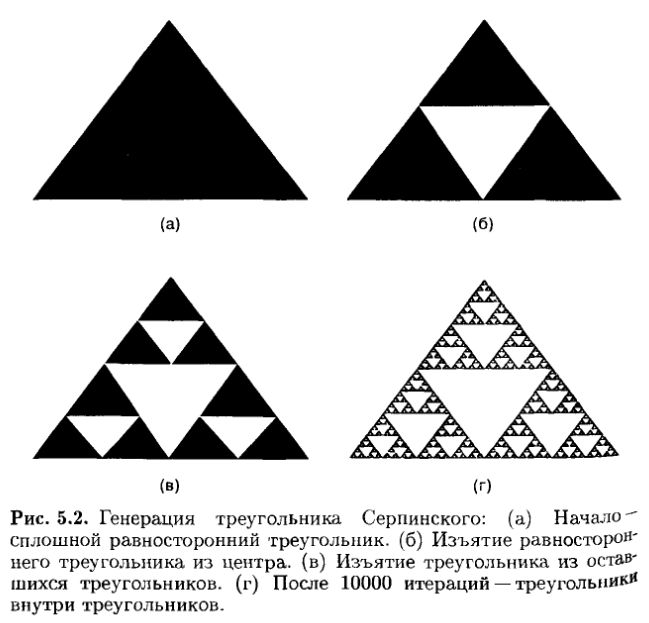
Далее удаляются треугольники из этих малых сплошных треугольников (рис. 5.2в). Если мы будем повторять этот процесс, то в итоге получим структуру, показанную на рис. 5.2г – треугольник, который имеет внутри себя бесконечное число уменьшенных треугольников. При увеличении какой-либо части этого треугольника можно было бы увидеть в ней еще больше уменьшенных треугольников. Таким образом, бесконечное число треугольников заключено в конечном пространстве исходного треугольника. При помощи простого правила в этом конечном пространстве создана бесконечная сложность. Этот особенный фрактал, называемый треугольником Серпинского, как мы увидим дальше, играет определенную роль в анализе временных рядов.

Теперь попытаемся применить к треугольнику Серпинского евклидову геометрию. Он не одномерный, так как не является линией. И не двумерный, как сплошной треугольник, ибо имеет в себе отверстия. Его размерность заключена между единицей и двойкой. Она равна 1.58 – это дробная, или фрактальная, размерность. Фрактальные размерности являются главными идентификационными характеристиками фракталов. Проницательную мысль Мандельброта о том, что фрактальная размерность существует естественным образом, можно сравнить с изобретением числа (0) (нуль) средневековыми восточными математиками, или с изобретением отрицательных чисел раннеиндийскими математиками. Фрактальные размерности – объективная реальность. Прежде не привлекавшие внимания, теперь они углубили и расширили дескриптивную мощь математики.

Мы склонны думать, что всякий плоский объект является двумерным. С точки зрения математики, это не так. Евклидова плоскость есть ровная поверхность без щелей и проломов. Подобным же образом мы склонны считать, что объект, имеющий «глубину» – является трехмерным. И снова, в евклидовой геометрии это не так. Трехмерный объект есть чистая сплошная форма. Математически он отличается свойством своей полной поверхности. Он не имеет в ней дыр и щелей. Следовательно, объект, обладающий глубиной, не обязательно является трехмерным. Например, фиксирующий шарнир представляет собой шар с углублениями; в соответствии с евклидовой геометрией он не является трехмерным, поскольку его поверхность не гладкая.

Обратимся к рассмотрению временного ряда фондовых цен, который представляет собой зазубренную линию. Она не одномерна, потому что не есть прямая. Но она также и не двумерна, поскольку не заполняет плоскость. На языке размерностей она более чем линия и менее чем плоскость. Ее размерность находится между единицей и двойкой. (В главе 9 мы установим, что эта кривая статистики S&Р 500 имеет размерность 1.24).

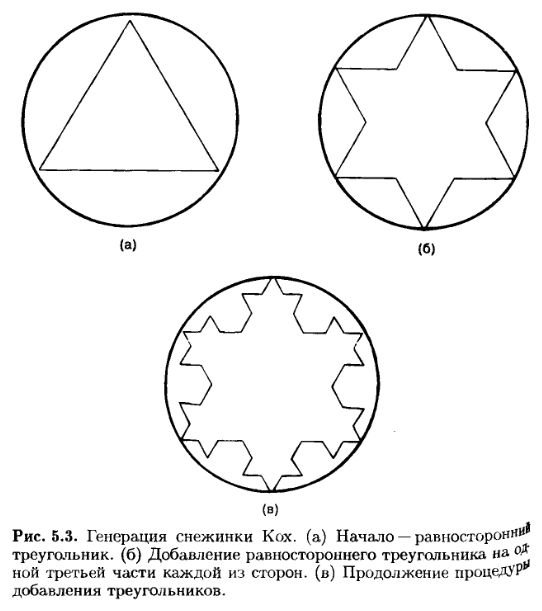
Другой пример фрактальной формы – снежинка Кох. Подобно треугольнику Серпинского, снежинка Кох создается аддитивным правилом. На рис. 5.3 показана эта процедура. Она начинается с равностороннего треугольника (рис. 5.3а). На средней трети каждой из сторон строится другой равносторонний треугольник, образуя форму, показанную на рис. 5.36. При повторении шага «б» получим в результате снежинку (рис. 5.3в). Такая снежинка, в принципе, имеет бесконечную длину, поскольку треугольники могут добавляться до бесконечности. Однако окружность, которая заключает в себе исходный треугольник, ограничивает это пространство. Мы имеем бесконечную длину внутри конечного пространства. И чем ближе мы будем рассматривать профиль этой снежинки, тем больше деталей увидим. Будут видны уменьшенные версии большой формы. Путем простого итеративного правила снова создан объект бесконечной сложности, заключенный внутри конечного пространства.

Два этих примера – треугольник Серпинского и снежинка Кох – являются симметричными фракталами. Они часто называются детерминистическими фракталами, потому что создаются с помощью детерминистических правил. Как мы установили, естественные объекты в действительности никогда не бывают симметричными. Две рассмотренные фрактальные формы, следовательно, не представляют природные формы или рынки капитала, однако они иллюстрируют некоторые важные характеристики фракталов. Они являются объектами, созданными посредством простых итерационных правил, дающих самоподобные формы с фрактальными размерностями. Более реалистичными являются случайные фракталы.