|

Майкл Барнсли (Michael Bransley) из фирмы Itereted Systems, Inc., разработал математический аппарат для порождения фрактальных форм, который назвал итеративными функциональными системами (Iterated Function Systems – IFS). В одном из подмножеств IFS фракталы порождаются детерминистическим правилом, которое выполняется случайным образом. В результате появляется нечто такое, что трудно даже себе вообразить. Барнсли назвал свой алгоритм игра хаоса.
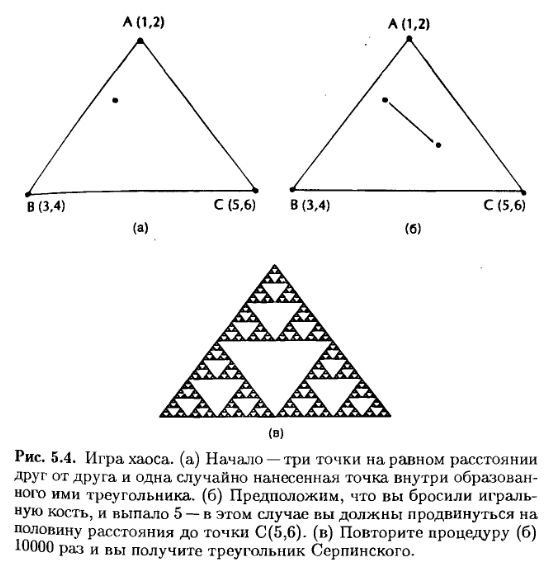
Одна из форм игры хаоса показана на рис. 5.4. Начинается игра с трех равноотстоящих точек (рис. 5.4а). Пометим точку А как (1,2), точку В как (3,4) и точку С как (5,6). Это игровая доска. Выберем теперь некоторую точку внутри треугольника АВС.
Чтобы сыграть в эту игру, бросаем игральную кость (убедитесь, что кость имеет правильную форму). Продвинемся на половину пути до точки, номер которой выпал. Например, если выпало 5, пройдем половину отрезка до точки С (5,6) и нанесем новую точку, как это показано на рис. 5.46.
Проделаем так 10000 раз (используя компьютер). Примерно после 10 000 итераций придем к результату, показанному на Рис. 5.4в, который нам уже знаком, ибо это не что иное как треугольник Серпинского – несмотря на то, что точки получены совсем другим способом. И в том и в другом случаях нанесение каждой точки зависит от положения всех предыдущих точек. И в том и в другом случаях получается треугольник Серпинского. Как это может быть?
Барнсли говорит, что этот треугольник есть предел данной IPS. Он является аттрактором системы.
Давайте рассмотрим, как осуществляется эта игра хаоса.
Информация, выдаваемая игральной костью, случайна. Система не знает, куда она двинется до того, как выпадет очередная цифра. Предсказать направление здесь невозможно. Но получив информацию, процесс направляется внутренним детерминистическим правилом. Результатом является целый диапазон возможностей, но количество возможностей бесконечно. Эта структура – бесконечные возможности внутри конечного диапазона – есть аттрактор, или предел, множества, задаваемого данной IFS.
Заметим, что этот аттрактор неслучаен, хотя он имеет бесконечное количество возможных решений. Каждая точка внутри треугольника появляется по-разному. Пространство внутри треугольника имеет нулевую вероятность обнаружить себя, хотя этих пространств – бесконечное количество.
Положение каждой точки зависит от того, где расположилась точка предыдущая. В действительности место каждой точки зависит от положения всех предыдущих, несмотря на то что информация, используемая при вычерчивании IFS, генерируется как случайная.
Как мы увидим в гл. 7, эта комбинация случайных событий и зависимости является характеристикой фрактальных временных рядов.
Так что же, следовательно, являет собой фрактал? Фрактал есть аттрактор (предельное множество) порождающего правила (информационного процессора). Это – некое самоподобие, в котором меньшие части соотносятся с целым. Оно имеет фрактальную размерность. Это более сложное определение, чем приведенное ранее. Однако не существует абсолютно точного определения фрактала. Возможно, когда-нибудь оно будет найдено, но такого может и не случиться ввиду того, что фрактальная геометрия есть геометрия природы. Дефиниция фрактала стоит в одном ряду с дефиницией природы.
Мы видели, что существует два типа фракталов: детерминистические и случайные. Детерминистические фракталы в большинстве случаев симметричны. Случайные фракталы не всегда включают в себя части, которые выглядят похожими на целое. Части и целое могут соотноситься качественно. Мы увидим, что фрактальные временные ряды качественно самоподобны, ибо в разных масштабах длительности они имеют одинаковые статистические характеристики. Если они проявляются как характеристики нормального распределения, значит налицо нормальное распределение. Однако фрактальный временной ряд может иметь только фрактальную размерность, в то время как размерность нормального распределения равна 2, а это меняет многие характеристики временного ряда.
Далее мы бегло рассмотрим концепцию фрактальной размерности. Она настолько важна, что достойна самостоятельной главы.
|