|

Страница, которую вы читаете, представляет собой трехмерный кусок бумаги. Предположим, что она не имеет толщины, а в действительности двумерна, т. е. является куском евклидовой плоскости. Если бы вы вырвали этот двумерный лист из книги и смяли в комок, то этот объем бумаги не был бы уже двумерным, но и не был бы в точности трехмерным. Бумага была бы вся в складках, и ее размерность была бы меньше трех. Чем больше спрессовывать бумагу, тем будет ближе ее размерность к трем, т. е. к размерности сплошного тела. Только если бы исходная страница была изготовлена из пластичного материала вроде глины, она, будучи сжата в комок, могла бы спрессоваться до истинно трехмерного тела. Но бумага всегда имеет складки.
Бумажный комок имеет дробную, или «фрактальную», размерность. Она не является целочисленной. Евклидова геометрия с ее чистыми гладкими формами не может описать размерность бумажного шара. Он не может быть представлен с помощью евклидовой геометрии кроме как посредством большого количества линейных интерполяций. В терминах математического анализа поверхность такого шара не дифференцируема.
Мы склонны думать обо всех объектах, которые имеют глубину, как о «трехмерных». С точки зрения математики, это неверно. Линия, прочерченная в трехмерном пространстве, имеет глубину, но эта линия остается одномерной. Истинно трехмерный объект – сплошное тело, не имеющее отверстий или трещин на своей поверхности. Вот почему представление естественных форм с помощью евклидовой геометрии является столь трудным. Большинство реальных объектов не сплошны в классическом, евклидовом смысле они имеют бреши и полости. Они просто располагаются в трехмерном пространстве.
Неспособность евклидовой геометрии описать большинство естественных объектов ограничивает нашу способность понять то, как объект устроен. Для случая временных рядов классическая геометрия не может оказать существенной помощи в понимании происхождения их структуры, если только это не случайное блуждание – система настолько сложная, что предсказать ее поведение невозможно. В терминах статистики число степеней свободы, или факторов влияния на систему очень высоко.
Фрактальная размерность, которая описывает, как объект (или временной ряд) заполняет свое пространство, является продуктом всех тех факторов влияния на систему, которые и порождают этот объект (или временной ряд).
Если камень случайным образом бомбардируется равномерно со всех сторон потоками воды, то по прошествии тысячелетия или двух он станет совершенно круглым. Каждая часть камня будет подвергнута равномерной эрозии. Количество потоков воды (или количество степеней свободы) может быть бесконечным.
Если количество таких потоков невелико, камень не станет гладким шаром. Если камень подвергается ударам воды только с некоторых сторон, он не станет круглым. Если будут три потока, то в камне окажутся три впадины. Если один поток будет интенсивнее других, то одна впадина будет глубже других.
В результате камень, подвергающийся эрозии большим количеством равной силы потоков, будет гладким, симметричным и – евклидовым. Камень со смещением в равномерности воздействий будет шероховатым и несимметричным.
Временной ряд будет только тогда случаен, когда он является следствием большого количества равновероятных событий. В терминах статистики – он имеет большое количество степеней свободы. Неслучайный временной ряд будет отражать неслучайную природу влияний. Скачки данных будут соответствовать скачкам влияющих факторов, отражая присущую им корреляцию. Иными словами, временной ряд будет фракталом.
Обычно мы помещаем объект в пространство, большее чем фрактальная размерность этого объекта. Мы полагаем, что шарик скомканной бумаги является трехмерным, хотя он не заполняет все отведенное ему трехмерное пространство.
Это пространство, рассматриваемое как объект, называется размерностью вложения, или топологической размерностью.
Когда объекты имеют размерность между двумя и тремя, мы склонны думать о них как о трехмерных. Примерами могут служить горы и облака.
Мы думаем о береговой линии как о двумерной, в то время как в действительности ее размерность меньше. Временной ряд относится к той же категории объектов. Только случайный временной ряд, который бы сплошь покрыл плоскость, был бы истинно двумерным.
Одна из характеристик фрактальных объектов состоит в том, что они оставляют себе свою собственную размерность, будучи помещены в пространство размерности, больше чем их фрактальная размерность. Случайные распределения (белый шум) не имеют этой характеристики. Белый шум заполняет свое пространство подобно тому, как газ заполняет объем. Если определенное количество газа поместить в контейнер большего объема, газ просто растечется в большем пространстве, поскольку молекулы газа ничто не связывает между собой. С другой стороны, твердое тело имеет молекулы, сцепленные друг с другом. Аналогично этому во фрактальном временном ряде положения точек определены корреляциями, но таких корреляций не существует в случайном ряде. Во фрактале, подобном треугольнику Серпинского, каждая точка коррелирована с точкой, нанесенной до нее. Если мы увеличим размерность пространства вложения треугольника, то корреляции останутся неизменными и будут стягивать точки в группы. Размерность треугольника останется неизменной, так же как осталась бы неизменной размерность временного ряда.
В случайном временном ряде нет корреляций точек. Ничто не удерживает точки в том же соседстве, сохраняя их размерность. Вместо того они целиком заполняют отведенное им пространство.
Фрактальная размерность определяется тем, как объект или временной ряд заполняет пространство. Фрактальный объект заполняет пространство неравномерно, поскольку его части зависимы, или коррелированы. Чтобы определить фрактальную размерность, мы должны определить, каким образом объект группируется в единое целое в своем пространстве.
Существует много способов расчета размерности, но все они включают в себя подсчет объема или площади фрактальной формы и того, как она изменяется в масштабах в том случае, если этот объем или форма увеличиваются.
Береговые линии являются хорошим примером, особенно если провести параллель между ними и временными рядами. Мандельброт (1982) выдвинул постулат о том, что мы никогда не сможем измерить действительную длину береговой линии, поскольку измеряемая длина зависит от длины используемой для измерения линейки.
Предположим, например, что мы хотим измерить длину побережья штата Мэн. Мы начнем с самой северной точки и будем мерить, накладывая на поверхность земли линейку шестифутовой длины. Мы будем складывать шестифутовые приращения, двигаясь вниз по берегу, и придем к какому-то числу. Затем мы повторим эту процедуру, используя трехфутовую линейку. На этот раз мы сможем уловить больше деталей, так как линейка наша короче. Поскольку мы сможем учесть большее количество бухточек и фиордов, мы в итоге получим большую длину побережья. Если мы укоротим линейку еще на один фут, то получим еще больше деталей и еще большую длину. Чем короче будет становиться линейка, тем длиннее береговая линия. Получается, что длина береговой линии зависит от размеров линейки!
Ввиду того что это справедливо для всех береговых линий, длина как мера не годится для сравнения береговых линий. Вместо нее Мандельброт предложил использовать фрактальную размерность. Береговые линии представляют собой зазубренные кривые, поэтому их фрактальная размерность больше единицы (т. е. их евклидовой размерности); то, насколько она больше единицы, зависит от степени зазубренности. Чем она больше, тем ближе размерность береговой линии к двум – размерности плоскости
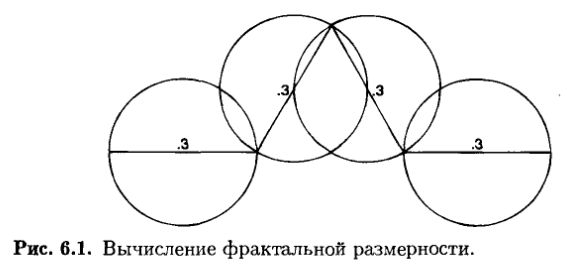
Фрактальная размерность рассчитывается посредством измерения этого свойства зазубренности. Мы подсчитываем количество окружностей определенного диаметра, которое необходимо для покрытия береговой линии. Мы увеличиваем их диаметр и снова считаем их количество. Продолжая эту процедуру, мы найдем, что количество окружностей и их радиус связывает показательная зависимость:

где N – количество окружностей, r –радиус окружности, D – фрактальная размерность.
Уравнение (6.1) может быть приведено к отношению логарифмов:
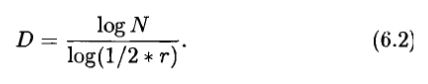
Можно использовать некоторую часть снежинки Кох в качестве простейшей береговой линии; средняя треть этой линии несет на себе равносторонний треугольник. Если длина этой ломаной цепочки равна единице, то тогда нам нужно четыре окружности диаметром 0.3, чтобы покрыть эту кривую (см. рис. 6.1). Фрактальная размерность кривой Кох будет равна:
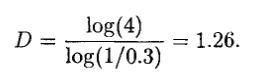
Реальные береговые линии устроены аналогичным образом. Береговая линия Норвегии, например, имеет фрактальную размерность, равную 1.52, в то время как берег Британии – 1.30. Это означает, что береговая линия Норвегии более изрезана, чем в Британии, и поэтому ее размерность ближе к 2.00. Подобным же образом мы могли бы сравнивать разные акции – посредством указания их фрактальных размерностей. Обычно мы сравниваем риски различных ценных бумаг посредством оценки их волатильности. Эта концепция была впервые широко представлена в работе Марковица (Markovitz, 1952); она предполагает, что чем выше волатильность акции, тем выше ее уровень риска. Волатильность, или риск, утверждался в качестве статистической меры, будучи представленным как стандартное отклонение прибылей – или их квадратов, т. е. дисперсий. Волатильность предлагают измерять дисперсией прибылей, не так ли?
Стандартное отклонение измеряет вероятность того, что наблюдение будет располагаться на определенном расстоянии от среднего. Чем больше это расстояние, тем больше рассеяние. Большое рассеяние означало бы, что существует высокая вероятность больших колебаний прибыли. Такая ценная бумага обладает высоким уровнем риска. Однако часто упускают из виду, что стандартное отклонение как мера рассеяния подходит только для случайных систем. Если наблюдения коррелированы (или имеют серийную корреляцию), то тогда польза стандартного отклонения как меры рассеяния в значительной степени снижается. Поскольку многочисленными исследованиями установлено (см. гл. 3), что распределение прибылей акции не следует нормальному распределению, стандартное отклонение как мера сравнения уровней риска ставится под вопрос.
Рассмотрим для примера два ряда возможных прибылей, обозначенных S1 и S2 в таблице 6.1. Ряд S2 не нормально распределен и имеет выраженный тренд. Ряд S1 не показывает тренда и имеет накопленную прибыль 1.93%, в то время как S2 имеет 22.83%. Однако S1 имеет стандартное отклонение 1.70, в то время как S2 имеет фактически то же самое стандартное отклонение – 1.71. В этом гипотетическом примере две акции с фактическими одинаковыми волатильностями имеют совершенно различные характеристики прибылей. Пуристы скажут, что оба ряда не нормально распределены, и это делает их сравнение невозможным. Это совершенно верная точка зрения.

Поскольку прибыли акции явно не нормально распределены, использование стандартного отклонения как меры для сравнения рисков некорректно – так же как некорректно использование длины при сравнении береговых линий. Фрактальная размерность ряда S1 равна 1.41, ряда S2 – 1.13. Ряд S1 явно более зазубрен, чем S2, и его фрактальная размерность качественно отлична.
Две акции с одинаковой волатильностью, следовательно, могут иметь очень разные модели прибылей. Одна имеет «зыбкое» (почти случайное) поведение, вторая – персистентный тренд. Волатильность – не подходящая мера риска при сравнении этих двух ценных бумаг. Их фрактальные размерности дают нам другой взгляд на проблему, как это мы увидим в следующих главах.
ВЫВОДЫ
Фрактальная размерность показывает нам, как форма или временной ряд заполняют пространство. Способ заполнения объектом пространства определяется теми силами, которые определили его формирование. Для береговой линии такими силами выступает геологическая активность, обусловливающая ее формирование: давление ветра, вулканические явления и др. Для временного ряда прибыли акции – это микро- и макроэкономические факторы, влияющие на инвесторские ожидания. Различные акции могут по-разному реагировать на одни и те же макроэкономические новости по причине различий видов производств, балансов и перспектив. Заметим, что метод окружностей для определения фрактальной размерности неудобен в практическом отношении.
Мы пока еще не исследовали влияние фрактальной размерности на вероятностные распределения. Мы видели, что фрактальные формы и временные ряды характеризуются долговременными корреляциями. Они не следуют с необходимостью случайным блужданиям. Их вероятностное распределение не является нормальным распределением (хорошо известной изящной кривой), но являет собой другую форму.
В следующих главах мы изучим это влияние долговременных корреляций на временные ряды, которое порождает фракталы. Мы увидим, что наше статистическое определение риска как стандартного отклонения прибылей нуждается в серьезной корректировке.
|