Показатель Херста

Херст был гидрологом, который начал работать над проектом нильской плотины около 1907 г. и прожил в регионе Нила почти сорок лет. Все это время он занимался проблемой резервуарного контроля. Идеальный резервуар никогда не должен переполняться. Стратегия, которая могла бы быть положена в основу управления, состоит в ежегодном спуске определенного количества воды. Однако, если приток из реки будет слишком мал, уровень воды в резервуаре может стать опасно низким. Проблема заключалась в том, какой сброс выбрать, чтобы резервуар никогда не переполнялся и не оставался пустым.

При создании модели было выдвинуто общее предположение о том, что неуправляемая часть системы – в данном случае приток воды от дождей – следует случайным блужданиям. Это обычное предположение, которое выдвигается в отношении больших систем со многими степенями свободы. Экология нильского бассейна не была исключением. Поистине, она содержала множество степеней свободы!

Когда Херст решил проверить это предположение, он в результате дал нам новую статистику – показатель Херста (H). Как мы увидим, этот показатель имеет широкое применение в анализе временных рядов благодаря своей замечательной устойчивости. Он содержит минимальные предположения об изучаемой системе и может классифицировать временные ряды. Он может отличить случайный ряд от неслучайного, даже если случайный ряд не гауссовский (т. е. не нормально распределенный). Херст обнаружил, что большинство природных систем не следуют случайному блужданию – гауссовскому или какому-либо иному.

Херст измерял колебания уровня воды в резервуаре относительно среднего с течением времени. Можно было ожидать, что диапазон этих флуктуаций будет меняться в зависимости от величины временного промежутка измерений. Если ряд случайный, размах будет увеличиваться пропорционально корню квадратному из времени. Это – уже упоминавшееся правило T^1/2. Для калибровки этих временных измерений Херст ввел безразмерное отношение посредством деления размаха на стандартное отклонение наблюдений. Этот способ анализа стал называться методом нормированного размаха (R/S-анализ). Херст показал, что большинство естественных явлений, включая речные стоки, температуры, осадки, солнечные пятна следуют «смещенному случайному блужданию» – тренду с шумом. Сила тренда и уровень шума могут быть оценены тем, как изменяется нормированный размах со временем, или, другими словами, насколько величина H превосходит 0.5.

Мы намерены распространить метод Херста изучения временных рядов природных явлений на временные ряды в экономике и на рынках капитала, чтобы выяснить, являются ли эти ряды также смещенными случайными блужданиями. Для переформулирования работы Херста применительно к обобщенным временным рядам мы должны прежде всего определить размах, который был бы сравним с колебаниями уровня в резервуаре:

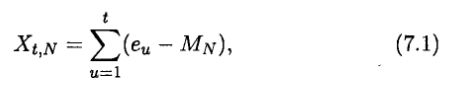
где X_{t, N} – накопленное отклонение за N периодов, е_u – приток в году u, M_N – среднее e_u за N периодов. Тогда размах становится разностью между максимальным и минимальным уровнями, достигнутыми в (7.1),

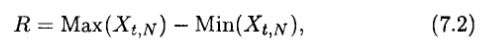
где R – размах отклонения X, Мах(Х) – максимальное значение для X, Min(X) – минимальное значения для X.

Для сравнения различных типов временных рядов Херст разделил этот размах на стандартное отклонение исходных наблюдений. Этот «нормированный размах» должен увеличиваться со временем. Херст ввел следующее соотношение:

где R/S – нормированный размах, N – число наблюдений, a – константа, H – показатель Херста.

В соответствии со статистической механикой показатель H должен был равняться 0.5, если ряд представляет собой случайное блуждание. Другими словами, размах накопленных отклонений должен увеличиваться пропорционально квадратному корню из времени N. Когда Херст применил свою статистику к записи стоков Нила, он нашел H = 0.90! Он испытал другие реки. Значение H было обычно больше 0.50. И для других природных явлений, во всех случаях Херст получил H больше чем 0.50. Что это означало?

Когда H отличается от 0.50, то это значит, что наблюдения не являются независимыми. Каждое наблюдение несет память о всех предшествующих событиях. Это не кратковременная память, которую часто называют «марковской». Это другая память – долговременная, теоретически она сохраняется навсегда. Недавние события имеют влияние большее, чем события отдаленные, но остаточное влияние этих последних всегда ощутимо. В долговременном масштабе система, которая дает статистику Херста, есть результат длинного потока взаимосвязанных событий. То, что случается сегодня, влияет на будущее. То, где мы находимся теперь, определяется тем где мы были в прошлом. Время оказывается важным фактором. Подобно тому как галька увлекается текущей водой сегодняшние события устремляются в будущее. Сила этого стремления постепенно ослабевает – до тех пор, пока все его цели и намерения не сведутся к нулю.

Включение «стрелы времени» невозможно в стандартной эконометрике, которая предполагает ряды инвариантными по отношению к времени. В противоположность этому мы находим, что время – итеративный процесс, подобный игре хаоса в гл. 5. Влияние настоящего на будущее может быть выражено корреляционным соотношением:

где С – мера корреляции, Н – показатель Херста.

Имеются три различных классификации для показателя Херста: 1) H = 0.5, 2) 0 ≤ H < 0.5, 3) 0.5 < H < 1.0. H, равное 0.5, указывает на случайный ряд. События случайны и некоррелированны. Правая часть уравнения (7.4) обращается в нуль. Настоящее не влияет на будущее. Функция плотности вероятности может быть нормальной кривой, однако это не обязательное условие. R/S-анализ может классифицировать произвольный ряд, безотносительно к тому, какой вид распределения ему соответствует. В курсах статистики нам говорят, что природа следует нормальному распределению. Открытие Херста это положение опровергает. Показатель H, как правило, бывает больше 0.5, а вероятностные распределения не являются нормальными.

Перед тем как изучить этот класс, стоит кратко обсудить случай 0 < H < 0.5. Данный диапазон соответствует антиперсистентным, или эргодическим, рядам. Такой тип системы часто называют «возврат к среднему». Если система демонстрирует рост в предыдущий период, то скорее всего в следующем периоде начнется спад. И наоборот, если шло снижение, то вероятен близкий подъем. Устойчивость такого антиперсистентного поведения зависит от того, насколько H близко к нулю. Чем ближе его значение к нулю, тем ближе С в уравнении (7.4) к -0.5, или отрицательной корреляции. Такой ряд более изменчив, или волатилен, чем ряд случайный, так как состоит из частых реверсов спад-подъем. Несмотря на широкое распространение концепции возврата к среднему в экономической и финансовой литературе, до сих пор было найдено мало антиперсистентных рядов.

При 0.5 < H < 1.0 мы имеем персистентные, или трендоустойчивые ряды. Если ряд возрастает (убывает) в предыдущий период, то вероятно, что он будет сохранять эту тенденцию какое-то время в будущем. Тренды очевидны. Трендоустойчивость поведения, или сила персистентности, увеличивается при приближении H к единице, или 100% корреляции, в соотношении (7.4). Чем ближе H к 0.5, тем более зашумлен ряд и тем менее выражен его тренд. Персистентный ряд – это обобщенное броуновское движение, или смещенные случайные блуждания. Сила этого смещения зависит от того, насколько H больше 0.5.

Персистентные временные ряды являют собой более интересный класс, так как оказалось, что они не только в изобилии обнаруживаются в природе, – это открытие принадлежит Херсту, – но и свойственны рынкам капитала. Однако, что выступает причиной персистентности? Почему ряды обладают эффектом памяти?