|
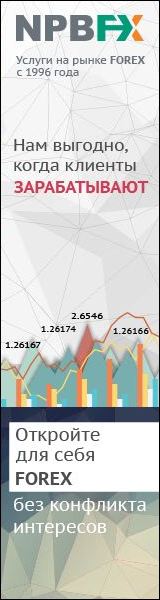
Персистентный временной ряд, определенный для 0.5 < Н ≤ 1.0 является фракталом, поскольку может быть описан как обобщенное броуновское движение. В обобщенном броуновском движении существует корреляция между событиями на временной шкале. Вследствие этого вероятность двух событий, следующих одно за другим, не 50/50. Показатель Херста Н описывает такую вероятность, при которой два происходящих последовательно события могут быть одинаковыми. Если Н = 0.6, существует, в принципе, большая вероятность того, что если предшествующее движение было положительным, то оно и останется положительным еще какое-то время. Это не истинная вероятность, это просто мера «смещения».
Поскольку точки (события) временного ряда не равновероятны (ввиду того что порождаются случайным блужданием), фрактальная размерность вероятностного распределения не равна 2, ее величина лежит в диапазоне от 1 до 2. Мандельброт (1972) показал, что величина, обратная Н, есть фрактальная размерность. Случайное блуждание при Н = 0.5 должно иметь фрактальную размерность, равную 2. Если Н = 0.7, фрактальная размерность равна 1/0.7, или 1.43. Заметим, что случайное блуждание в действительности Двумерно и целиком заполняет плоскость.
На рис. 7.1 показан имитационный ряд при Н = 0.52, 0.72 и 0.90. Когда Н приближается к 1, ряд становится менее зашумленным и имеет больше последовательных наблюдений с одинаковым знаком. На рис. 7.2 те же данные представлены в виде накопленного временного ряда.
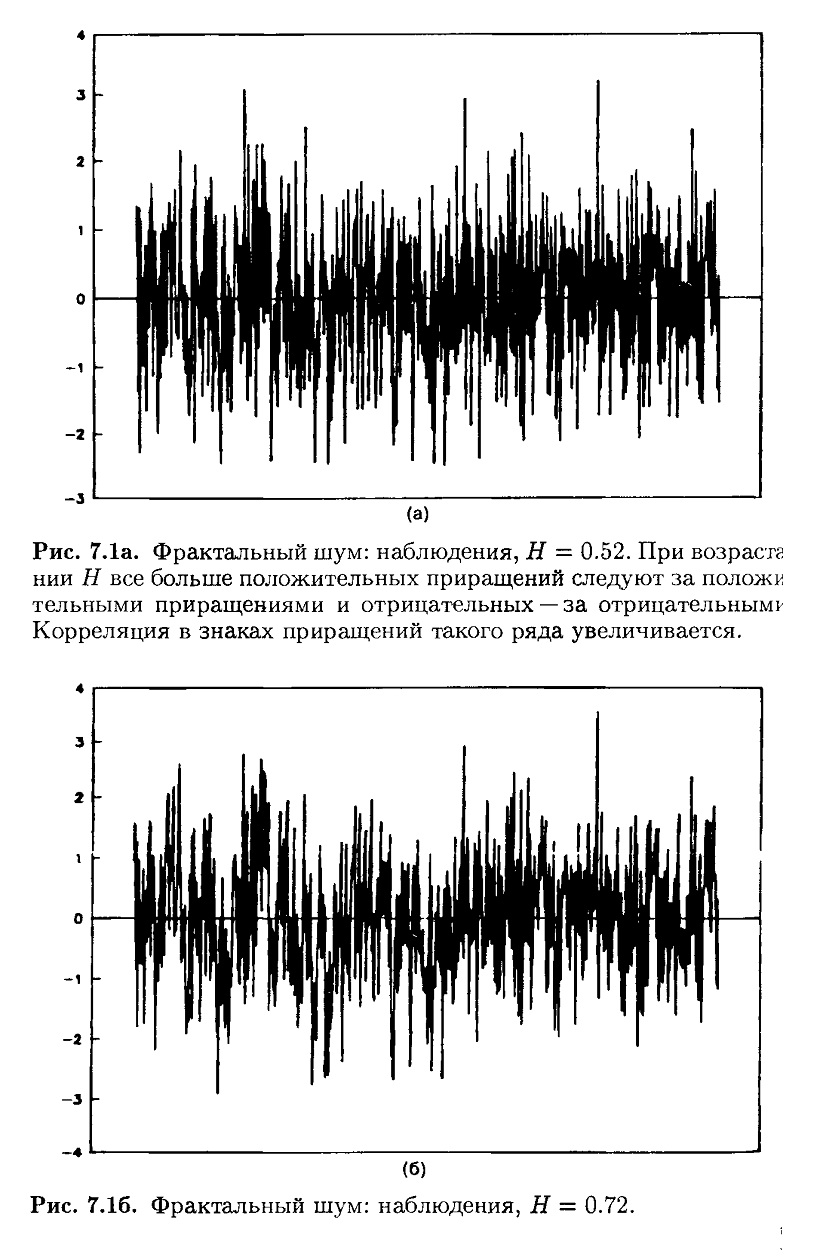
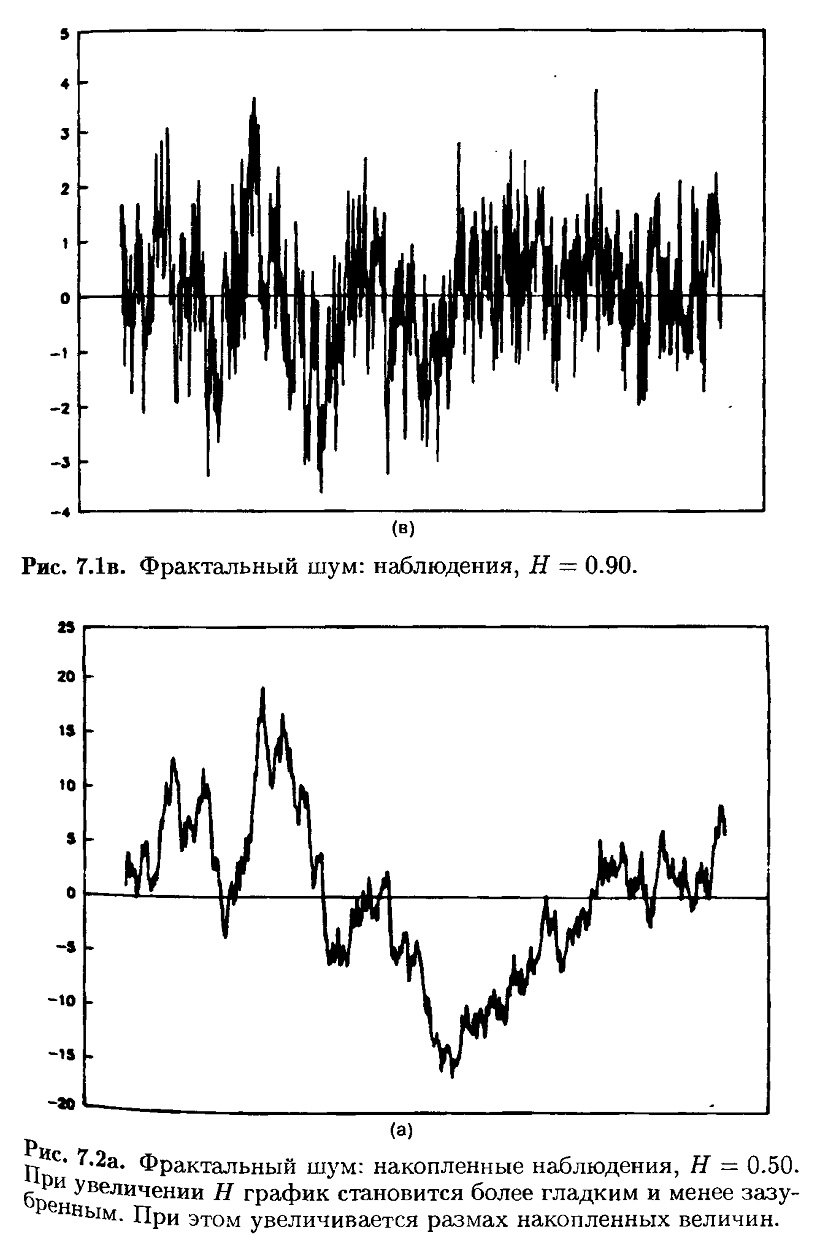
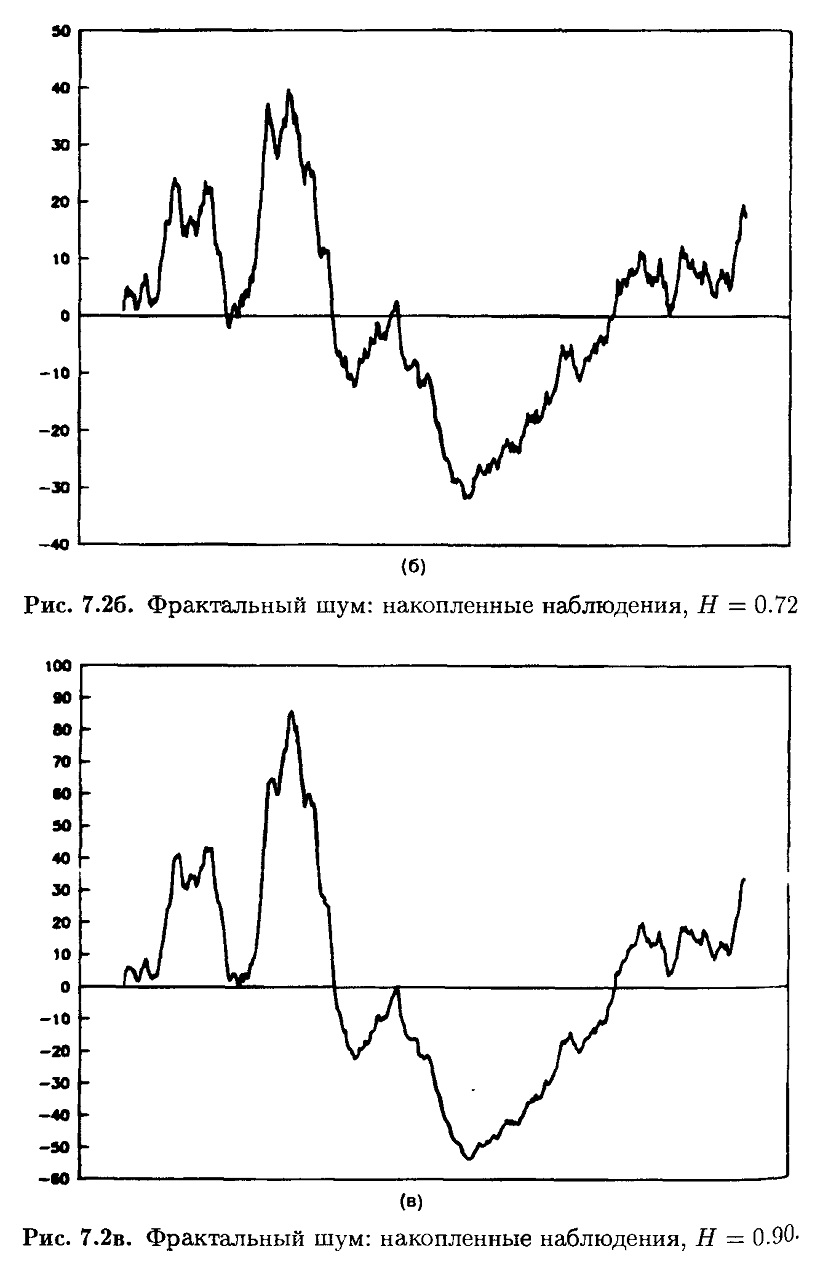
И снова, если Н увеличивается, накопленная кривая становится плавнее и менее зазубрена. Здесь меньше шума, и «тренды», или отклонения от среднего, более выражены. Показатель Херста Н является мерой зазубренности временного ряда. Совершенно детерминированная система должна порождать гладкую кривую. Фрактальный временной ряд как бы отделяет ряд чисто случайный от детерминированной системы, возмущенной случайными событиями.
В Приложении 3 дано краткое описание бейсик-программы для имитации ряда обобщенного броуновского движения с помощью ряда гауссовского. Этот метод помогает понять, кроме того, что представляет собой обобщенное броуновское движение. Каждое приращение во временном ряду обобщенного броуновского движения вычисляется как скользящее среднее, со степенной весовой функцией, от гауссова процесса с п независимыми случайными числами. С каждым шагом весА предшествующих N наблюдений уменьшаются; N олицетворяет собой эффект долговременной памяти системы; теоретически она бесконечна. Для целей имитации мы должны ограничить ее произвольно выбранным большим числом. В демонстрационном примере ряд из 8000 псевдослучайных чисел преобразован в 1400 смещенных случайных чисел описанным выше методом. Каждое смещенное приращение состоит из 5 случайных чисел и памяти о 200 смещенных числах. Проверка показала, что программа обладает достаточным быстродействием. Для каждого смещенного приращения (которое состоит из 5 гауссовских чисел) мы должны оценить 200 предшествующих смещенных чисел (5 * 200 = 1000 гауссовских чисел). Эффект памяти порождается включением в расчет текущего числа, предшествующих чисел. Если рынок обладает подобного Рода эффектом памяти, то тогда каждая прибыль соотносится с величинами предшествующих М прибылей. В любом случае измерение Н далее ведет к описанной выше несложной, хотя и довольно громоздкой вычислительной процедуре.
|