|

Прологарифмируем соотношение (7.3):
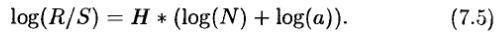
Если в двойных логарифмических координатах найти наклон R/S как функцию от N, то тем самым мы получим оценку Н. Эта оценка не связана с какими-либо предположениями относительно лежащего в основе распределения.
Для очень большого количества наблюдений N можно ожидать сходимости ряда к величине Н = 0.50, так как эффект памяти уменьшается до того уровня, когда становится незаметным. Другими словами, в случае длинного ряда наблюдений можно ожидать, что его свойства станут неотличимы от свойств обычного броуновского движения, или простого случайного блуждания, поскольку эффект памяти рассеивается. Регрессия в этом случае должна выполняться до того, как Н приблизится к 0.5, так как корреляционная мера (7.4) не применима ко всем без исключения приращениям.
Важно напомнить, что корреляционная мера (7.4) не имеет отношения к автокорреляционной функции гауссовских случайных переменных. Последняя предполагает гауссовские или почти гауссовские свойства лежащего в основе распределения – хорошо знакомую красивую кривую. Автокорреляционная функция хорошо работает в определенных краткосрочных зависимостях, однако имеет тенденцию преуменьшать долгосрочные корреляции в негауссовских рядах. Читателям, интересующимся полным математическим объяснением того, почему автокорреляционная функция не дает хороших результатов в процессах с долговременной памятью, рекомендуем обратиться к статье Мандельброта (1972).
На рис. 7.3 в двойных логарифмических координатах представлена кривая зависимости R/S от N для Н = 0.5, построенная по данным из рис. 7.1. Эти данные были получены с помощью генератора псевдослучайных чисел с гауссовским выходом и показывают Н = 0.55 ± 0.1. Эта оценка немного выше, чем ожидалось, но эти псевдослучайные числа сгенерированы детерминистическим алгоритмом. Это может быть причиной смещения. Важно заметить, что R/S-анализ – это исключительно устойчивый метод. В его основе нет предположения о гауссовском распределении. Найденное значение Н = 0.50 не является доказательством того, что налицо гауcсовское случайное блуждание, оно доказывает только то, что это процесс, который отличается короткой памятью. Другими словами, любая независимая система, гауссовская или какая-либо другая, может продуцировать Н = 0.5.?
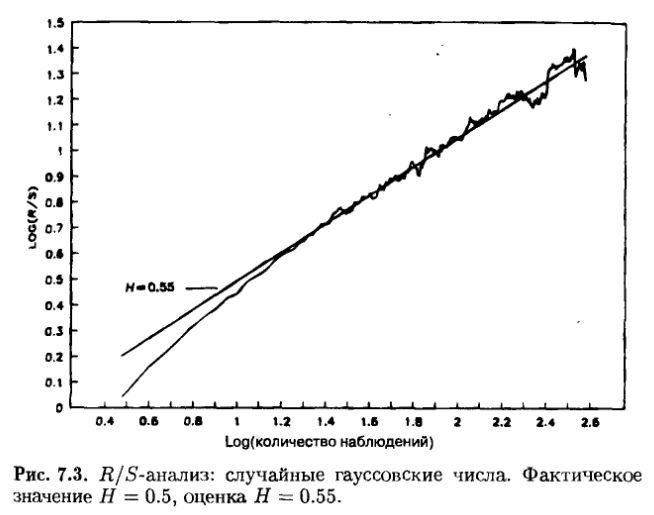
На рис. 7.4 показана аналогичная кривая для Н = 0.72 – значения, часто наблюдаемого в природных процессах. Эти данные (они также представлены на рис. 7.1) были получены аппроксимацией обобщенного броуновского движения, более детально описанной в Приложении 3. Такой ряд получен, как было сказано, с учетом памяти о 200 наблюдениях. В имитаторе Херста, использующем смещенную колоду из 27 карт, эффект памяти моделировался джокером. Он мог появляться, в среднем, после 27 снятий колоды, в продолжение большого количества имитаций. Имитатор Херста располагал памятью о 27 наблюдениях. Долгосрочные корреляции после 27- наблюдений падают до нуля, и при шаге по времени 27 наблюдений или более система начинает следовать случайным блужданиям. Таким образом, мы могли бы принять эти 27 наблюдений как цикл, или период, системы. Данные, которые были взяты для построения кривых на рис. 7.1 и 7.2, имитируют естественный цикл из 200 наблюдений.
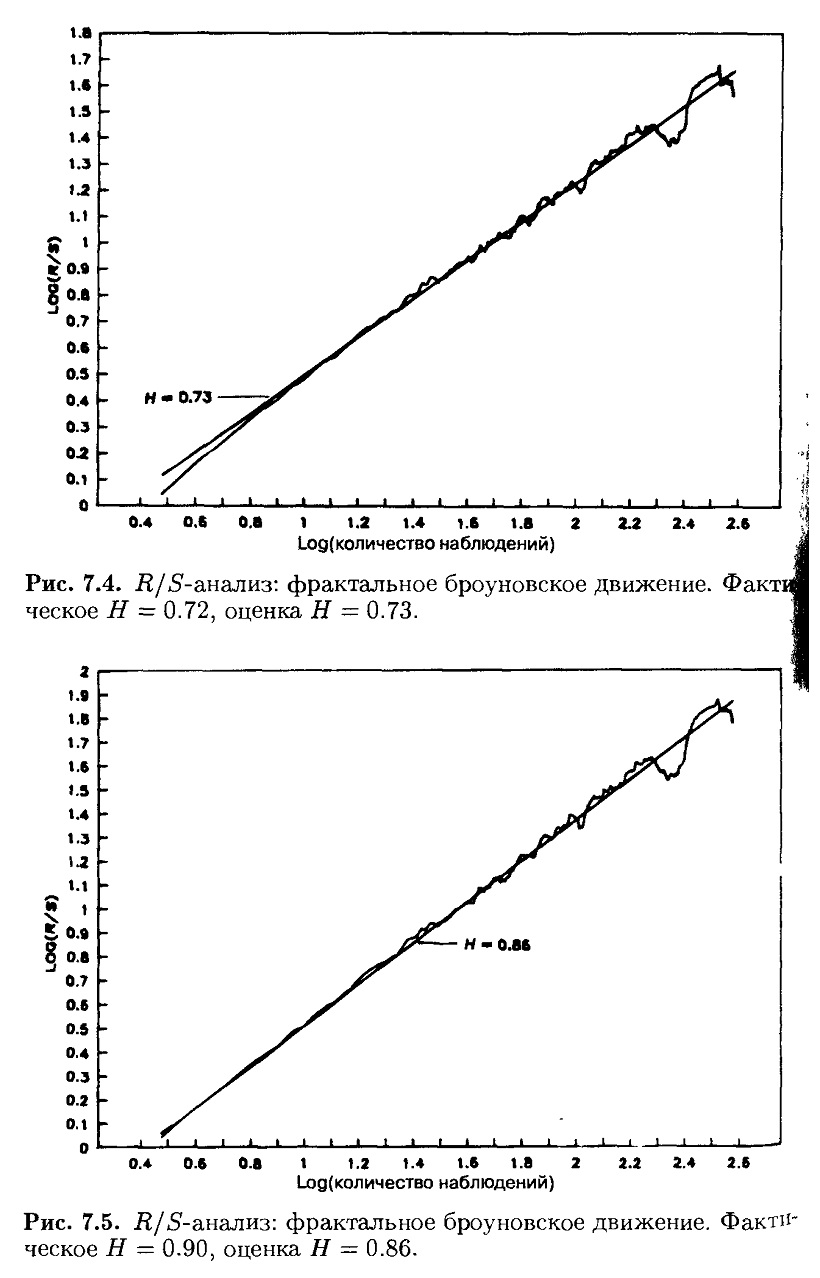
Когда мы превышаем N = 200 (log(200) = 2.3), тогда R/S-наблюдения становятся сбивчивыми и случайными. Это свойство R/S-анализа позволяет нам определить среднюю длину цикла системы. В терминах нелинейной динамики систем средняя длина цикла есть длительность, по истечении которой теряется память о начальных условиях. На рис. 7.5 показана аналогичная кривая, построенная для Н = 0.90. Действительная Н в этом случае оказалась немного ниже, но в допустимых пределах.
|