|
ЭМПИРИЧЕСКИЙ ЗАКОН ХЕРСТА
Херст (1951) предложил также формулу для оценки величины Н по значению R/S:
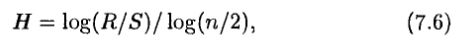
где n – количество наблюдений.
В этой формуле предполагается, что константа α из соотношения (7.5) равна 0.50. Федер (Feder, 1988) показал, что этот эмпирический закон имеет тенденцию преувеличивать Н, когда оно больше 0.70, и, наоборот, преуменьшать, если Н ≤ 0.40, однако для коротких рядов, где регрессия невозможна, этот эмпирический закон может быть использован как разумное приближение.
ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ И Н
Фрактальная размерность временного ряда, или накопленных изменений при случайном блуждании, равна 1.50. Фрактальная размерность кривой линии равна 1, а фрактальная размерность геометрической плоскости равна 2. Таким образом, Фрактальная размерность случайного блуждания лежит как бы на полпути между кривой линией и плоскостью.
Показатель Херста может быть преобразован во фрактальную размерность с помощью следующей формулы:

Таким образом, если Н = 0.50, то D = 1.50. Обе величины характеризуют независимую случайную систему. Величина 1 < Н ≤ 0.50 будет соответствовать фрактальной размерности, более близкой к кривой линии. Это, по терминологии Херста, персистентный временной ряд, дающий более гладкую, менее зазубренную линию, нежели случайное блуждание, как мы видели на рис. 7.26 и 7.2в. Антиперсистентная величина H (0 < H < 0.50) дает соответственно более высокую фрактальную размерность и более прерывистую линию, чем случайное блуждание, и, следовательно, характеризует систему, более подверженную переменам. Это в точности соответствует антиперсистентному временному ряду.
|