|

Перед тем как в следующей главе мы начнем рассматривать рынки капитала, будет полезным применить R/S-анализ к какому-либо временному ряду реальных данных из области природных систем.
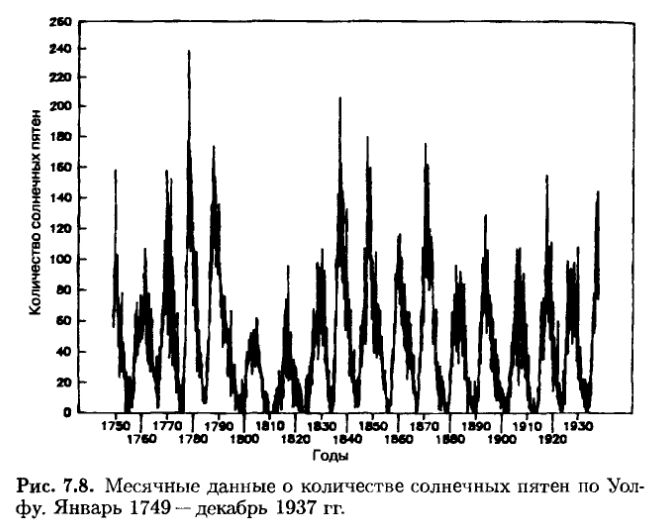
Возможно, наиболее широко известной естественной системой с непериодическим циклом являются циклы солнечных пятен. Данные о количестве солнечных пятен записываются с середины восемнадцатого века, когда Вольф завел порядок ежедневных наблюдений солнечного диска и записи количества солнечных пятен на его поверхности. Когда он умер, Цюрихская обсерватория продолжила эту практику, и делает это по сей день. По методике Вольфа совокупность нескольких близко расположенных пятен считается одним большим пятном. Таким образом, пять пятен вчера могут стать одним большим пятном сегодня. В сочетании с ошибками, присущими ручным процедурам, процесс такого подсчета ведет к определенной измерительной погрешности. К тому же количество пятен имеет в высшей степени асимметричное распределение: оно может почти приближаться к нулю (и это случалось неоднократно), но его максимум может быть сколь угодно велик. Циклы количества солнечных пятен считаются непериодическими со средней продолжительностью в 11 лет.
Солнечные пятна являют собой временной ряд, весьма подходящий для R/S-анализа ввиду того, что мы имеем запись их длительной истории. В моей библиотеке есть старая книга Харлана Тру Стетсона (Harlan The Stetson) «Солнечные пятна и их эффекты», опубликованная в 1938 г. Она содержит таблицу месячных данных о солнечных пятнах с января 1749 г. по декабрь 1937 г. Мандельброт и Уоллис (Mandelbrot, Wallis, 1969в), а также Херст уже проделали аналогичную работу. Однако полезно ввести некоторые изменения в методику в соответствии с нашими предыдущими исследованиями. Прошу заметить, что я не устанавливаю какой-либо связи между циклом солнечных пятен и циклами рынков капитала или экономики в целом. Я анализирую цикл солнечных пятен как таковой
На рис. 7.8 представлены месячные данные о количестве солнечных пятен как временной ряд. Заметим, что хотя эти «Циклы» видны невооруженным глазом, временной ряд носит скачкообразный характер. R/S-анализ применен к логарифму разности количества пятен от месяца к месяцу.
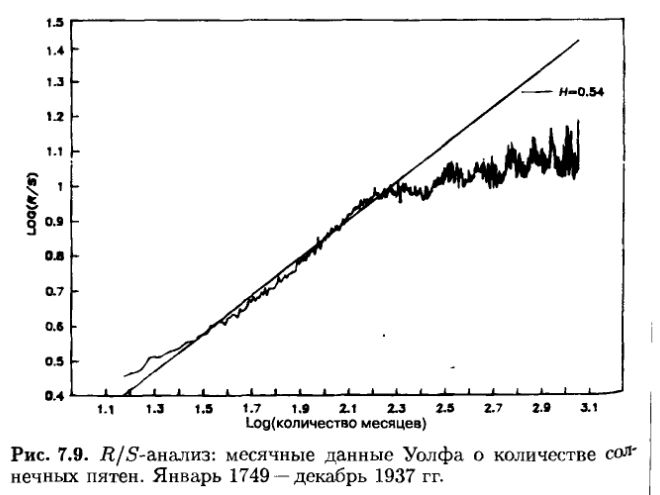
На рис. 7.9 в двойной логарифмической шкале построена кривая R/S как функция от времени. По ней можно видеть, что периоды, короче 12-13 лет, имеют показатель Херста, равный 0.55. Факт отсутствия больших отклонений говорит о персистентном поведении ряда. Наконец, наклон кривой резко падает, свидетельствуя о том, что эффект долговременной памяти диссипирует через 10-13 лет. Это приблизительно совпадает с 11-летней оценкой цикла, которая принята в науке.
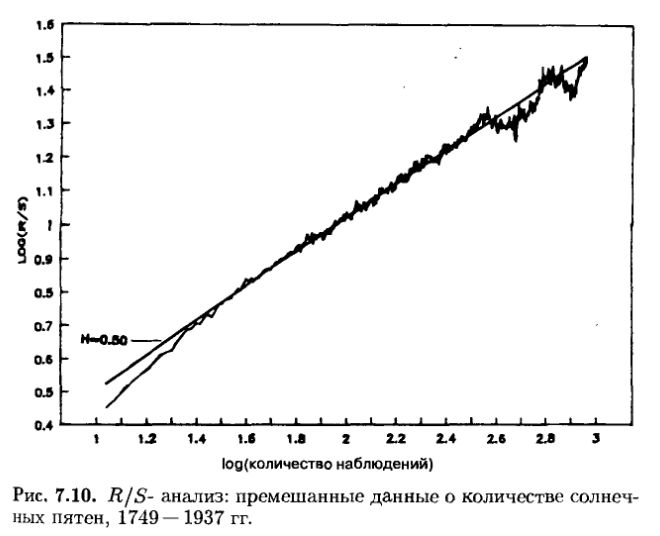
На рис. 7.10 показан результат теста на перемешивание месячных данных временного ряда. Показатель Херста теперь равен 0.50, и след долговременной памяти оказывается полностью затертым.
На этом примере можно видеть, что естественные системы могут обладать свойствами долговременной памяти, как это предполагается в модели обобщенного броуновского движения. Однако эта память не бесконечна – она велика, но ограничена. Этот результат подобен отношению между природными и математическими фракталами. Как мы видели, масштабная инвариантность математических фракталов безгранична, как при уменьшении, так и при увеличении размеров. Однако фракталы природные характеризуются остановкой скейлинга на некотором фиксированном масштабе. Ответвления в легких животных, например, не становятся бесконечно малыми. Подобно этому, фрактальные временные ряды имеют долгую, но конечную память. При рассмотрении рынков капитала и экономических временных рядов мы обнаружим те же характеристики. Экономические временные ряды, как и ряды показателей на рынках капитала, демонстрируют долгую, но конечную память. Мы также увидим, что длительность циклов этой памяти изменяется от рынка к рынку и от одной ценной бумаги к другой.
ВЫВОДЫ
Из рассмотрения метода нормированного размаха – R/S- анализа – можно выделить два важных с информационной точки зрения показателя: показатель Херста Н и среднюю длину цикла. Существование длины цикла имеет важное значение для оценки инерции движения. Величина Н, отличная от 0.5, означает, что вероятностное распределение не нормально. Если 0 < Н < 1, то ряд является фракталом. Поведение фрактального временного ряда отличается от случайных блужданий. Мы рассмотрели понятия персистентности и долгосрочных корреляций, но существуют и другие отличия в его характере; мы рассмотрим их внимательно в гл. 9. Теперь же перейдем к рынкам капитала.
|