|

В этой главе мы рассмотрим различие между фрактальным и нормальным вероятностными распределениями. В частности, обобщим математику, лежащую в их основе, и покажем, что нормальная форма является частным случаем фрактальных распределений. С точки зрения математического аппарата данная глава, возможно, не покажется интересной для всех читателей. Однако, ввиду того что фрактальные распределения приобретают большое значение в современных рынках капитала, как минимум три последних раздела и заключение главы рекомендуем внимательно изучить.
ПАРЕТО (ФРАКТАЛЬНЫЕ) РАСПРЕДЕЛЕНИЯ
Фрактальные распределения известны достаточно давно. В экономической литературе они носят названия «Парето», или «Парето-Леви», или «устойчивые паретовские» распределения. Свойства этих распределений первоначально были изучены Леви и опубликованы в 1925 г. Его работа основана, в свою очередь, на наблюдениях Парето (1897), касающихся распределения доходов. Последним было обнаружено, что доход хорошо аппроксимируется логнормальным распределением, за исключением приблизительно трех процентов наивысших индивидуальных доходов. На этом участке доход начинает следовать обратному степенному закону, что дает утолщение хвоста. Грубо говоря, вероятность того, что один человек в десять раз богаче другого, подчиняется нормальному распределению, но вероятность стократного превышения благосостояния оказывается намного больше той, что предсказывается нормальным распределением.
Парето предположил, что этот утолщенный хвост, вероятно, возникает потому, что богатый может более эффективно умножать свое богатство, чем средний индивид, чтобы достичь более высокого благосостояния и более высоких доходов. Похожий обратно-степенной закон был найден Ципфом (G. К. Zipf, 1948) для частот используемых слов. Ципф обнаружил, что длинные слова используются реже, чем короткие. Лотка (A. J. Lotka, 1926) приводит примеры обратно-степенных законов из области социологии, один из них – публикации научных статей в академических журналах. Чем больше статей опубликовал академик, тем более вероятна его публикация. Это происходит потому, что интенсивность публикаций подкрепляется учащимися студентами: большинство хорошо известных и старых членов академии могут быть соавторами, тем самым увеличивая свою продуктивность. Во всех перечисленных случаях утолщенные хвосты несут на себе влияние обратной связи, которая увеличивает продукцию – в каких бы единицах она ни измерялась. Эффект обратной связи усиливает событие и делает хвосты даже длиннее. Леви взял эти «толстохвостые» распределения и обобщил все вероятностные распределения таким образом, чтобы включить их в общую картину.
Перед тем как приступить к изучению фрактальных распределений, рассмотрим некоторые характеристики нормальных распределений. Большинство из нас так или иначе имели дело с нормальным распределением. Хорошо знакомая изящной формы кривая широко используется – достаточно того, что в некотором смысле все мы были проранжированы «на кривой» еще в школе. Эта кривая описывается формулой, и можно записать логарифм характеристической функции нормального распределения случайной переменной t:
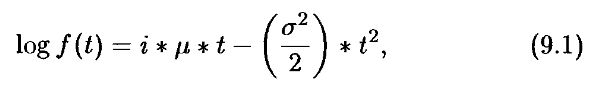
где μ
– среднее,
σ2 – дисперсия.
Для этого «стандартного нормального» распределения среднее равно нулю и стандартное отклонение (квадратный корень из дисперсии) равен единице. Поскольку нормальное распределение применяется, когда t является независимой, идентично распределенной (IID) случайной переменной, оно применимо к броуновскому движению и случайным блужданиям.
Как установлено в гл. 2, Башелье первым выдвинул идею о том, что спекулятивные рынки следуют случайным блужданиям и могут быть смоделированы как игра случая. Гауссовская гипотеза Башелье продолжает приниматься на веру, несмотря на то, что очевидный эмпирический факт указывает на аномалию отличия от случайных блужданий – об этом говорилось в гл. 3. В частности, частотное распределение прибыли постоянно проявляет большие отклонения, чем это должно было бы быть при наблюдениях в окрестности средней величины (см. рис. 3.1). Это распределение имеет более толстые хвосты и выше пик, чем у нормального распределения. Несмотря на это такое распределение часто описывается как «приблизительно нормальное».
Это «толстохвостое», островершинное распределение является характерной формой распределения Парето. Леви обобщил характеристическую функцию вероятностных распределений следующей достаточно сложной формулой:
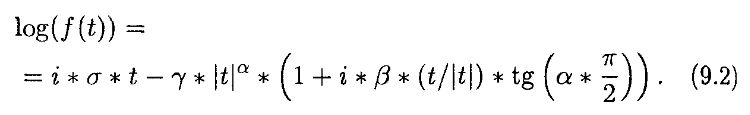
Эта формула имеет четыре характеристических параметра: α, β, δ, γ здесь δ – локальный параметр среднего, γ – масштабирующий параметр подгонки, например разница между дневными и недельными данными, β измеряет асимметрию и может изменяться от –1 до +1. Когда β = 0, распределение симметрично. Когда β = +1 распределение имеет толстый хвост справа, или скошено вправо. Степень правого скоса увеличивается при приближении β к +1. Обратное случается при β < 0; α измеряет островершинность распределения, так же как и толщину хвостов; α может изменяться в диапазоне величин от 0 до 2 включительно. Только при α = 2 это распределение становится эквивалентным нормальному. Полагая в (9.2) α = 2, β = 0, γ = 1 и δ = 1, получаем уравнение (9.1) – характеристическую функцию нормального распределения. Гипотеза эффективного рынка (ЕМН) предполагает, в сущности, что α всегда должно быть равно 2. Гипотеза фрактального рынка (FMH) утверждает, что α может изменяться в диапазоне от 1 до 2. В этом состоит основное различие между двумя гипотезами рынка. Однако изменение величины α драматически изменяет характеристики временных рядов.
Мы полагаем распределение Парето фрактальным, потому что оно статистически самоподобно по отношению к времени. Если распределение дневных цен имеет среднюю величину m и α = а, то распределение пятидневных прибылей должно иметь среднее значение 5 * т и при этом должно остаться α = a. Будучи выполненной, масштабная временная подгонка должна оставить форму вероятностного распределения временного ряда без изменения. Такой временной ряд называется масштабно-инвариантным. Подобное описание применимо, если α = 2 и распределение является нормальным, потому что нормальное распределение есть особый случай в семействе фрактальных распределений. Однако при а, не равном 2, характеристики распределения изменяются.
Во-первых, когда 1 ≤ α < 2, дисперсия становится неопределенной, или бесконечной. Дисперсия конечна и устойчива только при α = 2. Следовательно, дисперсия выборки является важной информацией только в том случае, если система представляет собой случайное блуждание. С другой стороны, бесконечная дисперсия возможна и, быть может, типична. Если α не равно 2, дисперсия выборки как мера рассеяния или риска практически не несет никакого смысла.
Если 0 < α ≤ 1, то тогда также не существует устойчивого среднего. Альфа редко лежит в этом диапазоне, но несколько позже мы столкнемся с одним таким примером. Однако при 1 < α ≤ 2 имеется устойчивая средняя величина. Нецелые альфа в этом диапазоне соответствуют смещенным броуновским движениям, которые характеризуются долговременными корреляциями и статистическим самоподобием. Эти движения являются фракталами. В дополнение к этому а есть фрактальная размерность пространства вероятностей временного ряда и

где H – показатель Херста.
Заметим, что, являясь фрактальной размерностью, α отличается от фрактальной размерности D в уравнении (7.7). D есть фрактальная размерность временного следа, в то время как альфа есть фрактальная размерность пространства вероятностей. D измеряет «зазубренность» временного ряда, α – толщину хвостов в функции плотности вероятности.
Фрактальные распределения имеют две другие интересные характеристики. Мандельброт назвал первую «Иосиф-эффектом». Как показано раньше, это название обязано тенденции фрактальных распределений иметь тренды и циклы. В Библейской истории рассказывается как Иосиф истолковал сон фараона: семь лет изобилия последуют за семью годами голода.?
Вторую характеристику Мандельброт назвал «Ной-эффект» – по имени героя Библейского предания о Всемирном потопе. В технической интерпретации это синдром бесконечной дисперсии. Такие системы склонны к внезапным драматическим переменам. В нормальном распределении большие изменения случаются по причине большого количества малых изменений. Изменение цен полагается непрерывным. Это предположение о непрерывности ценообразования делает страхование портфеля возможной практической стратегией денежного управления. Идея состояла в том, что, используя модель расчета цен опционов Блэка-Шоулса (или какую- то ее разновидность), инвестор мог искусственно повторять выбор, непрерывно балансируя между рисковыми активами и наличными деньгами. Этот метод правдоподобен постольку, поскольку ценообразование остается непрерывным, или по крайней мере близко к этому. Однако в случае фрактального распределения большие перемены происходят как следствия малого количества больших изменений. Большие изменения цен могут быть разрывными и внезапными. Фрактальное распределение на фондовом рынке могло бы объяснить, почему октябрьские события 1987, или 1978, или 1929 годов вообще случились. На этих рынках недостаток ликвидности стал причиной внезапного и прерывистого ценообразования, как это и предсказывает фрактальная модель. Мы воочию увидели в гл. 8, что рынки капитала имеют фрактальные распределения.
|