Инвариантность относительно сложения

Другим свойством устойчивых распределений является то, что, изменяясь в масштабах, они должны сохранять свои статистические свойства при сложении. Например, если ряд изменений дневных цен был нормально распределенным со средней величиной т и дисперсией s², то тогда изменения декадных цен должны также быть нормально распределенными со средней 10 * т и дисперсией 10 * s².

Если же распределение дневных цен было фрактальным, то распределение декадных цен должно иметь среднюю величину, равную 10 * т, но при этом дисперсия не останется устойчивой. В то же время величина показателя Херста Н для декадных прибылей будет той же, что и для прибылей дневных.

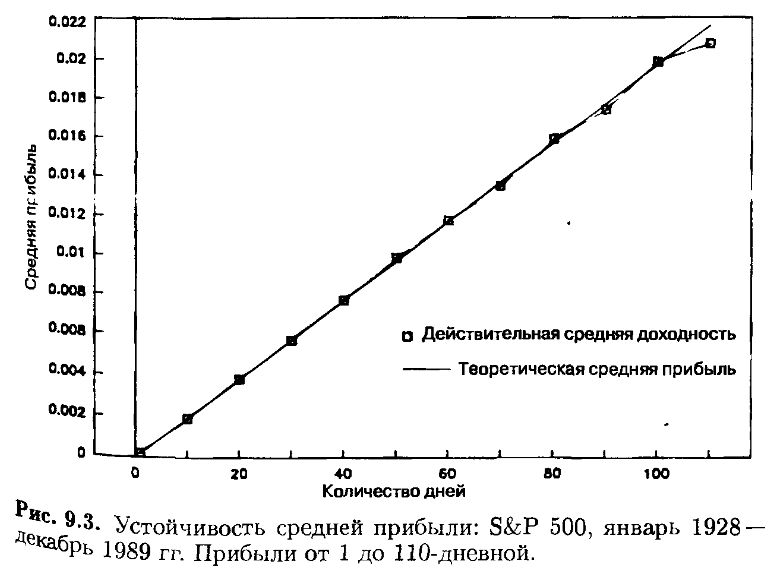
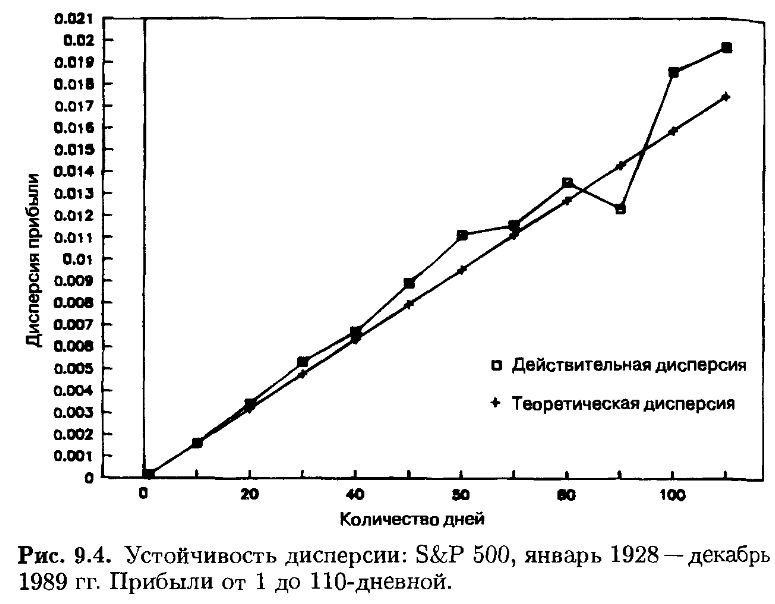
Для проверки этой возможности я создал ряд из 80-ти однодневных логарифмических прибылей, используя данные о дневных ценах S&P 500. Это подлинные и равномерные приращения прибылей. Были также обработаны месячные данные, при этом месяц принимался равным 1/12 года, несмотря на то, что месяцы имели три различных длины в днях и другие несоответствия. Для теста были использованы приращения по торговым дням. «Дыры» от уикендов и каникул были проигнорированы, не считаясь торговыми днями. Во-первых, было проверено свойство скейлинга для средних величин и дисперсий. Результаты для средних представлены на рис. 9.3, для дисперсий – на рис. 9.4. Средние ведут себя почти в точности так, как предсказывает теория, дисперсии были несколько выше. Дисперсия была также несколько более хаотична, чем это должно быть. Это означает, что гауссовская гипотеза становится проблематичной.

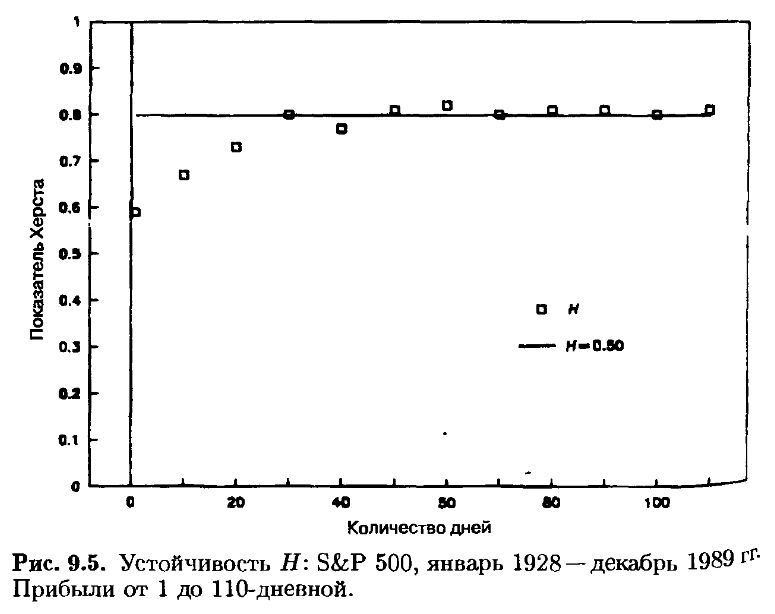
На рис. 9.5 показаны величины показателя Херста Н, вычисленные по тем же данным. Теоретически Н должно быть одинаковым для всех смещений. Реальность, однако, снова не укладывается в теорию. Величина Н неуклонно возрастает от 0.59 для однодневных приращений до 0.78 для 30-дневных приращений. Далее она колеблется в диапазоне от 0.78 до 0.81 по всем приращениям. Это означает, что в системе имеется шум для периодов короче 20 дней. Примерно между 20 и 30 днями (или около одного месяца) шум исчезает и Н сходится к величине, примерно равной 0.78 – мере для календарных месяцев, найденной в гл. 8. Происхождение шума при величинах Н, меньших 0.78, мы попытаемся объяснить позже.

Длина цикла оказалась неожиданно однородной. Она проявляется в диапазоне от 900 до 1100 дней, т. е. составляет примерно четыре года. На рис. 9.6 это проиллюстрировано для 20-дневных прибылей.

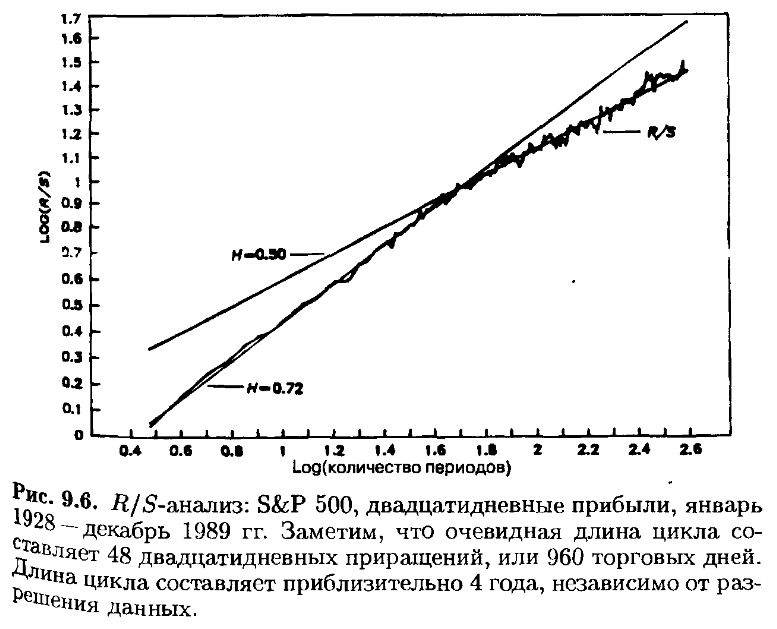
Этот четырехгодичный цикл не зависит от разрешения данных. «Джокер» появляется в среднем каждые четыре года, рассматриваем ли мы однодневные или более длинные периоды. Другими словами, дело не в том, какое количество точек мы имеем, а в том, сколько периодов охватывают эти данные. Это в корне отличается от стандартного статистического анализа, где более важно количество точек, нежели длина исследуемого временного ряда. Следовательно, дневные данные за четыре года, или 1040 наблюдений, не дадут такого замечательного результата, какой могут дать месячные данные за сорок лет, или всего 480 наблюдений.

Причина здесь в том, что дневные данные образуют только один цикл, а месячные – десять циклов. Из этого следует, что надо быть очень внимательным к стандартам, которые мы применяем в нелинейном анализе. Обычный метод привлечения большого количества данных помогает в анализе только тогда, когда исследуется IID (независимые идентично распределенные данные). Тогда время не имеет значения – в противоположность количеству наблюдений. Однако нелинейные системы имеют стрелу времени. Время не может быть повернуто вспять, и длина временного периода более важна, чем разрешение данных. Фактически увеличение разрешения часто делает анализ более затруднительным, но не повышает значимость результатов.

Итак, мы обнаружили два факта в подкрепление гипотезы фрактального рынка (FMH):

1. Показатель Херста Н, который является величиной, обратной по отношению к фрактальной размерности, устойчив для независимых периодов времени. Четыре десятилетних периода дали однородные величины Н, – это впечатляющий результат, если принять во внимание то, как изменился мир за последние 60 лет.

2. Для приращений, больших или равных 30 дням, FMH дает приблизительно равные величины Н, колеблющиеся между 0.78 и 0.81.

Однако имели место и некоторые сюрпризы. При разрешении, большем 30 дней, мы получили меньшую величину Н. Чем больше приращение, тем больше величина Н, пока мы не достигнем 30-дневного периода. Кроме того, была обнаружена конечная величина памяти (четыре года), безотносительная к разрешению данных. Я хотел бы остановиться на этих двух моментах.

Более низкая величина Н может наблюдаться в тех случаях, когда имеется большой случайный шум в данных или явление «возвратных значений». Из этого следует, что движение в дневных ценах акций больше подвержено возвратам, чем это свойственно им в более длинных временных периодах. Третье объяснение может состоять в том, что ценовые изменения в коротких временных периодах не независимы – как это утверждает фрактальная модель, но, напротив, содержат некоторые марковские кратковременные зависимости.

Мандельброт в 1963 г., изучая цены на хлопок, склонялся к этому третьему объяснению. Он замечал, что эти цены ведут себя не совсем так, как предсказывает теория. В частности: «... большие изменения не чередуются регулярно с периодами плавных перемен, они, похоже, склонны «промахиваться» и заходить дальше своих пределов. Подобным же образом ценовые изменения в периоды спокойствия выглядят более гладкими, чем это предсказывает фрактальный процесс».

Другими словами, большие изменения цен следуют своим законам, малые – своим. Мандельброт утверждает, что отдельные ценовые изменения не являются независимыми, как гласит его оригинальная модель, но содержат марковские кратковременные зависимости. Редкие резкие перемены, предсказанные оригинальной моделью, должны порождаться изменением периода колебаний. Периоды без резких изменений должны быть мягче. Такой процесс может дать значение Н ниже, чем процесс без марковских зависимостей, так как последние, будучи кратковременными, становятся слабее с увеличением временного приращения и при этом можно ожидать увеличения и стабилизации H. Приблизительно в течение месяца марковский процесс диссипирует, в результате чего H становится устойчивой величиной, равной 0.78.

Эта марковская зависимость не должна смешиваться с Долговременной зависимостью, или Иосиф-эффектом. Последний сохраняется постоянно, хотя он может быть неизмерим после цикла, когда теряется память о начальных условиях. Зависимость Херста означает, что сегодняшние события всегда продолжают влиять на будущее, и это влияние никогда не может быть устранено. Марковские зависимости быстро распадаются, обращаясь в шум.

Вторая неожиданность, состоящая в том, что четырехгодичный «цикл» независим от разрешения данных, имеет большое значение для количественного анализа. Во-первых, это означает, что долговременная зависимость может и должна измеряться с использованием месячных данных. Некоторые математические работы указывают на смещение, которое появляется при использовании малых выборок или коротких временных рядов. Однако, принимая во внимание этот подход к анализу временных рядов, мы должны помнить, что фрактальные распределения аддитивны. Каждый временной интервал имеет достаточное количество заключенных в течение него сделок. Таким образом, нам не требуется еще больше наблюдений. Что нужно – так это как можно более длинный временной ряд.

Все это имеет большое значение для исследований хаоса. Мы сможем использовать эту информацию – четырехгодичный цикл и редукцию до обычного шума в тридцатидневных интервалах – как помощь в нелинейном динамическом анализе.

В итоге, эти находки подчеркивают то обстоятельство, что мы должны пересмотреть многие методы статистической диагностики, которыми пользовались в прошлом. Очень немногие из них значимы в рамках нелинейного анализа, где независимость редка и поэтому нет оснований ее ждать.