|

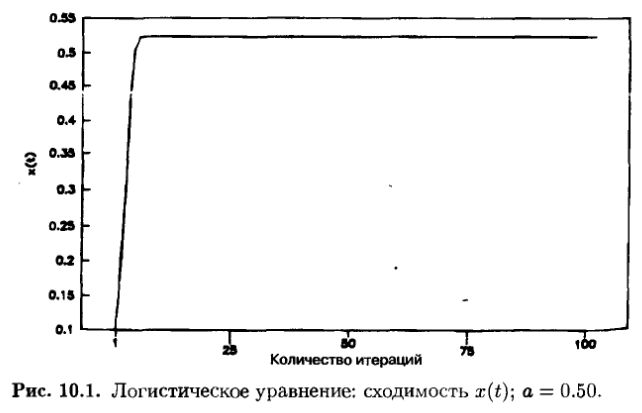
Рассматривая временные ряды с а = 0.5, мы можем увидеть, что после начального всплеска система устанавливается на одной устойчивой величине (рис. 10.1). Увеличение о до 0.6 снова демонстрирует сходимость ряда, однако на величине несколько большей.
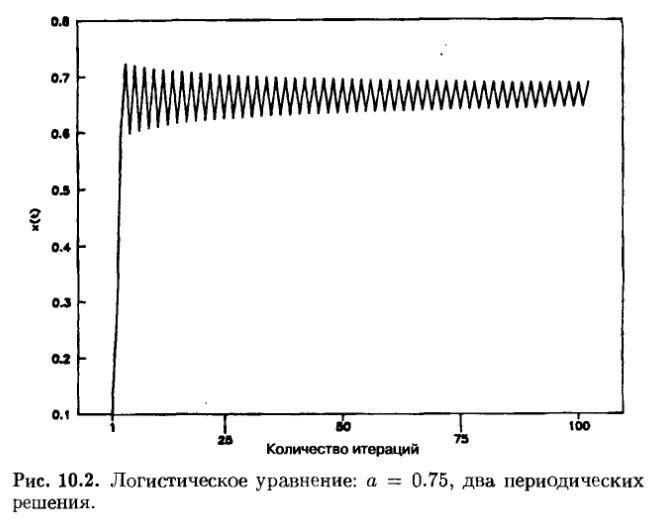
Увеличение а не дает ничего интересного до тех пор, пока мы не достигнем а = 0.75. Неожиданно система перестает устанавливаться на одной величине, а начинает осциллировать между двумя величинами (рис. 10.2). Это расщепление, переход от одного к двум потенциальным решениям называется бифуркацией
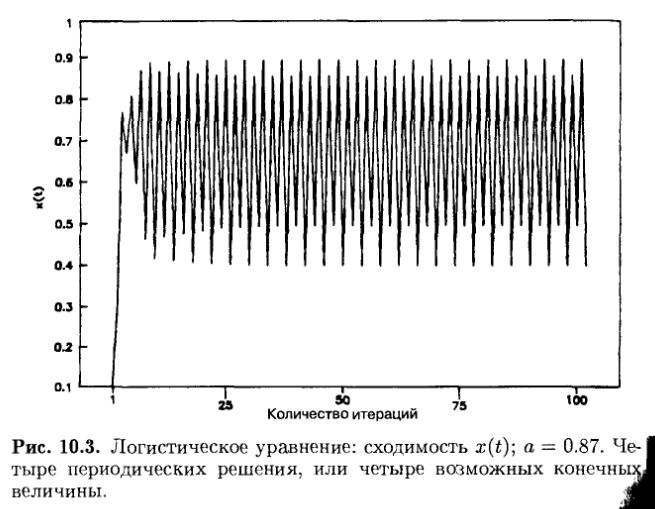
Если продолжить увеличение а, то приблизительно около 0.87 (точнее – 0.86237...) система вновь теряет устойчивость и появляются четыре возможных решения, как это показано на рис. 10.3. При дальнейшем увеличении а система будет вновь и вновь терять устойчивость. Критические величины а возникают все чаще и чаще и располагаются все ближе друг к другу. При а = 0.886 мы получаем восемь решений, при а = 0.8911 – шестнадцать, при а = 0.8922 – тридцать два, при а = 0.892405 – шестьдесят четыре решения. Это увеличение продолжается до а ~ 0.90 (точное значение – 0.892486418). Здесь происходит нечто удивительное.
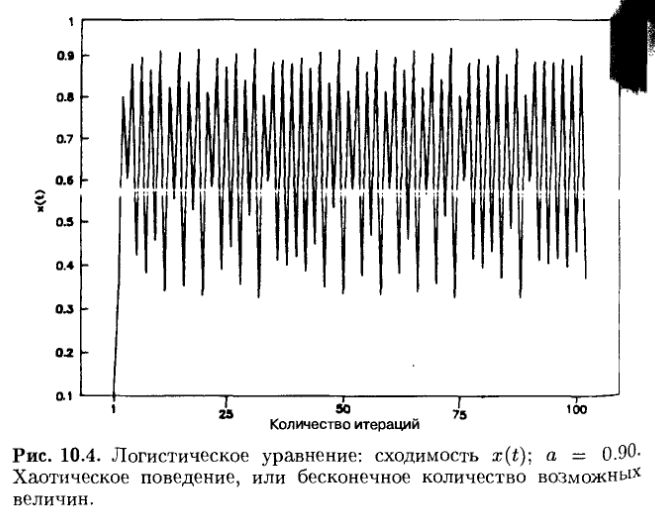
При а = 0.90 система полностью теряет устойчивость. Число решений становится бесконечным. При взгляде на временной ряд на рис. 10.4 мы видим хаос. Ряд выглядит случайным, и, если подвергнуть его статистическому анализу, то он таковым и окажется. Действительно, логистическое уравнение используется как датчик случайных чисел.
Примером физической системы, которая ведет себя подобно логистическому уравнению, является громкое вещание. Если микрофон воспринимает негромкую речь, можно услышать басовитое гудение. Если же громкость речи увеличивается, то в громкоговорителе внезапно начинают сменяться два фоновых тона. При дальнейшем увеличении громкости возникает еще больше бифуркаций, и на критическом уровне неуправляемая обратная связь приводит систему к аудиохаосу.
Это простое уравнение демонстрирует очень сложное поведение. Больше того, детерминистическое уравнение дает нам пример хаоса. Рассмотрим же его более внимательно.
|