Фазовое пространство

Визуальная оценка данных в нелинейных динамических системах важна потому, что они, как правило, не имеют единственного решения. Обычно существует множество – возможно, бесконечное количество – решений. Как и в реальной жизни, есть много возможностей. В прошлом это обстоятельство заставляло исследователей избегать рассмотрения нелинейных систем. Нынешние широкие графические возможности персональных компьютеров позволяют нам увидеть это огромное множество возможных решений. Многие хаотические системы имеют бесконечное количество решений, заключенных в ограниченной части пространства. Такого рода система тяготеет к определенной области пространства, и это множество возможных решений часто имеет фрактальную размерность. (Это самоподобие в игре хаоса Барнсли в гл. 5 осуществлено совершенно осознанно.)

Обозреть данные нетрудно, если нам известны все переменные системы. Мы просто наносим их на координатную плоскость. Если переменных две, то одну из них принимаем за х, другую за у и вычерчиваем зависимость в декартовых координатах, т. е. наносим величину одной из них относительно значения другой в один и тот же момент времени. Это называется фазовым портретом системы – он вычерчивается в фазовом пространстве. Размерность фазового пространства зависит от количества переменных в системе. Если она включает в себя две или три переменных, можно наблюдать данные визуально. Если размерность системы больше трех, то это делается математическими методами. Последний метод сложнее, но тем не менее осуществим.

Для нас важны три основных класса нелинейных систем. Каждый из них имеет свой собственный тип «аттрактора» (область решений) в фазовом пространстве.

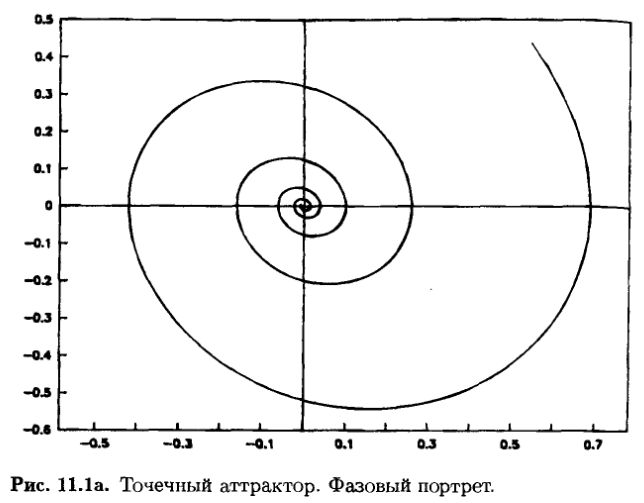
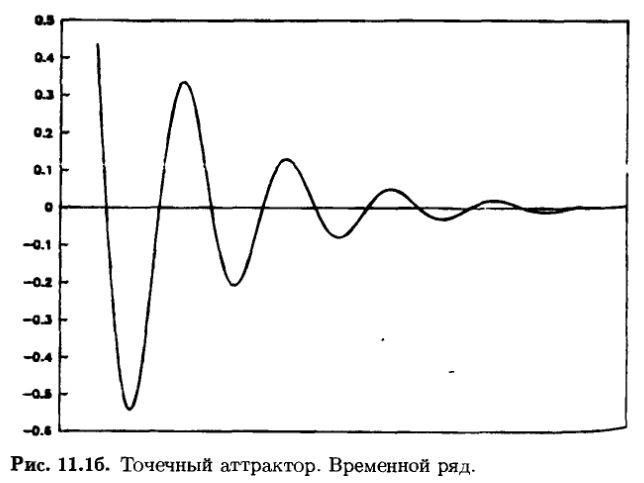
Простейшим типом является точечный аттрактор. Пример системы с точечным аттрактором – маятник, задемпфированный трением. Когда маятнику сообщается первоначальная энергия, он начинает раскачиваться, но ввиду трения амплитуда его колебаний становится все меньше и меньше, пока маятник совсем не остановится. Переменными в такой системе выступают скорость и положение. Если одну или другую из этих переменных вычертить как временной ряд, то результирующая волнистая линия будет постепенно уменьшать свою амплитуду до нуля – кривая становится прямой линией. Маятник останавливается. Это показано на рис. 11.16. Если фазовый портрет этой системы вычертить в координатах положение – скорость, то мы получим спиральную кривую, которая оканчивается в начале координат, когда маятник останавливается (см. рис. 11.1а). Если сообщить маятнику большую начальную энергию, временной ряд и фазовый портрет системы будут обладать большей начальной амплитудой, но тем не менее временной ряд придет к нулевому значению, а фазовый портрет – в начало координат. Можно сказать, что в этом фазовом пространстве система «притягивается» к началу координат. Где бы ни брала свое начало система, она приходит к началу координат – своему равновесному состоянию.

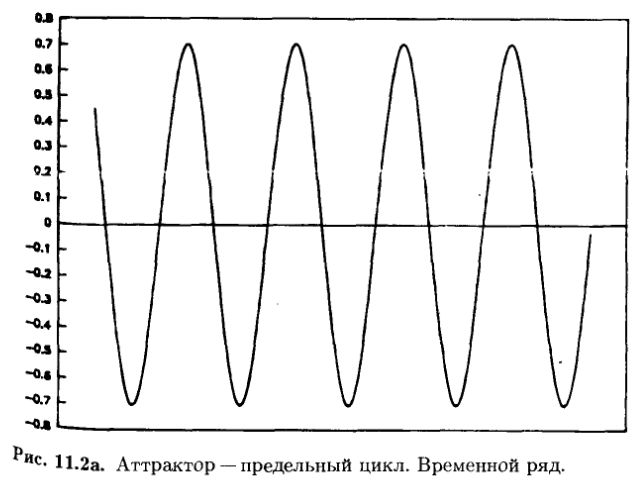
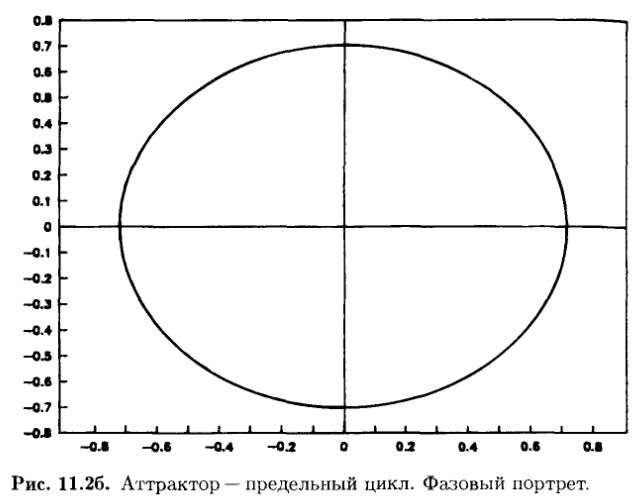
Предположим, что маятник не демпфирован. Сообщим ему толчок такой силы чтобы забросить в ту же исходную точку качания. В соответствии с ньютоновской физикой в данном случае будет иметь место аттрактор маятника, не задемпфированного трением или гравитацией. Временной ряд скорости или положения будет теперь синусоидой, как это показано на рис. 11.2а, а фазовый портрет – замкнутой окружностью (рис. 11.26).

Радиус этой окружности будет зависеть от силы «толчка», сообщенного маятнику, но окружность останется окружностью. Этот тип аттрактора, называемый предельным циклом, характеризует регулярную периодическую систему, в том числе маятник с притоком энергии извне.

Классическая эконометрика рассматривает экономические системы как системы равновесные (с точечными аттракторами) или как периодически колеблющиеся около точки равновесия (с аттракторами типа предельный цикл). Однако эмпирически такой взгляд не подтверждается. Экономические временные ряды характеризуются непериодическими циклами (т. е. не имеющими характеристической длины или временного масштаба). Такие непериодические циклы имеют место в нелинейных динамических системах.

Они доставляют нам последний тип аттрактора – хаотический, или «странный» аттрактор. Предположим, что мы случайным образом изменяем сообщаемую энергию, но время между толчками остается одинаковым. Влияние энергии будет теперь переменным и связано с силой предыдущего толчка, несмотря на то, что величины толчков относительно независимы. Поскольку мы сообщаем толчки энергии, случайные по своей силе, но через равные промежутки времени, положение и скорость маятника будут каждый раз отличаться. Если маятнику придать большую энергию первый раз, то во время второго толчка маятник может направляться уже вниз. Если этот второй толчок будет мал, то маятник может двигаться вверх, когда его настигнет третий толчок, который приведет к замедлению маятника. Несмотря на то, что мы продолжаем сообщать маятнику толчки энергии с регулярными интервалами, его фазовый портрет будет отличаться в каждом цикле.

Цикл от вершины до вершины качания характеризует собой орбиту. Поскольку маятник всякий раз не может завершить цикл, его фазовый портрет будет состоять из орбит, которые никогда не будут одинаковыми и не будут периодическими. Такой фазовый портрет выглядит случайным и хаотическим, но он ограничен определенными пределами (максимальной амплитудой маятника) и всегда будет вращаться по часовой стрелке, хотя размеры орбит и время их прохождения будут разными. Это хаотический, или странный, «аттрактор». Поскольку хаотические аттракторы к тому же имеют фрактальную размерность (как мы увидим позже), Мандельброт называет их «фрактальные аттракторы» – это название лучше нежели «странные», но оно не привилось. Странный аттрактор заключает в себе все возможности. Равновесие становится областью в фазовом пространстве – ограниченной областью с бесконечным количеством решений, подобно тому как это имеет место в треугольнике Серпинского и снежинке Кох.

Такое фазовое пространство дает нам картину возможностей системы. Для систем, уравнения которых известны, сконструировать фазовое пространство несложно. Если же природа системы неизвестна, а наблюдается только некий эффект, то фазовое пространство может быть восстановлено по данным. (Мы отложим обсуждение этой возможности до гл. 12.) В следующем разделе мы рассмотрим низкоразмерные системы с известными уравнениями. Они позволят нам изучить характеристики этого типа уравнений, перед тем как обратиться к временным рядам.