Фрактальная размерность

Фрактальная размерность фазового пространства мало отличается от фрактальной размерности временного ряда. Временной ряд будет иметь размерность между 1 и 2, поскольку мы имеем дело с единственной переменной. Фазовое пространство включает в себя все переменные системы. Его размерность зависит от сложности изучаемой системы.

Как было установлено в гл. 6, фрактальная размерность дает нам важную информацию относительно изучаемой системы. Целое число, непосредственно следующее за числом фрактальной размерности, говорит о минимальном количестве переменных, необходимых для моделирования динамики системы. Оно задает нижнюю границу возможного количества степеней свободы. Мы также установили, что фрактальная размерность D может быть аппроксимирована покрытием фрактала кругами и выводом следующей меры:

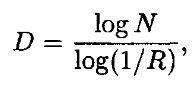
где N – количество кругов диаметра R.

Эта мера используется для фракталов в двумерном пространстве, подобных снежинке Кох. Для высокоразмерного аттрактора необходимо использовать гиперсферы размерностью 3 и выше.

Похожим, но более практичным методом, разработанным Грассбергером и Прокаччей (Grassberger, Procaccia, 1983), является нахождение корреляционной размерности, которая использует корреляционный интеграл C_m(R). Он представляет собой вероятность того, что две точки на аттракторе лежат в пределах расстояния R одна от другой.

Мы подсчитываем количество пар точек следующим образом. Во-первых, восстанавливаем наш временной ряд как фазовое пространство, начиная с нижней размерности вложения m = 2, как это было показано в предыдущем разделе. Затем, начиная с малого расстояния R, подсчитываем для него корреляционный интеграл C_m(R) в соответствии со следующим соотношением:

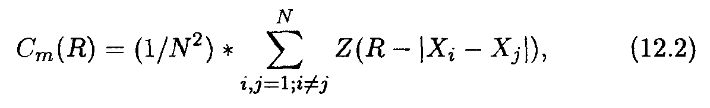
где Z(x) = 1, если R – |X_i – X_j| > 0, и равно 0 в противном случае N – количество наблюдений, R – расстояние. C_m – корреляционный интеграл для размерности т. Z(х) называется функцией Хевисайда, так как она равна 0, если расстояние между двумя точками X_i и X_j меньше R, и равна 1, если это расстояние большее. Корреляционный интеграл есть вероятность того, что две точки, выбранные случайным образом, удалены друг от друга меньше, чем на расстояние R. Если мы увеличиваем R, то C_m должно увеличиваться со скоростью R^D. Это дает следующее соотношение:

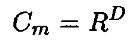
или

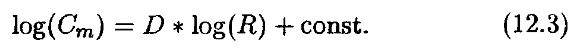
Для размерности т мы можем вычислять C_m при увеличении R. Находя наклон прямой на графике линейной регрессии в двойных логарифмических координатах log(C_m), log(R), мы можем оценить корреляционную размерность D для размерности вложения т. При увеличении т, размерность D будет в конце концов сходиться к своей истинной величине. По причинам, установленным выше, тот же результат имеет место, если размерность вложения становится больше, чем фрактальная размерность. Обычно сходимость наблюдается, когда размерность вложения на три или более целых чисел выше фрактальной размерности. Фрактал, вложенный в более высокую размерность, сохраняет свою истинную размерность по причине корреляций между точками. Таким образом, корреляционная размерность Грассбергера и Прокаччи является хорошей оценкой для фрактальной размерности. Эти две размерности, как показали названные авторы, прямо соотносятся друг с другом.

В Приложении 4 приведено описание бейсик-программы для расчета корреляционных интегралов по временным рядам. Ввиду того, что должны рассчитываться относительные расстояния между всеми точками ряда, эта программа работает сравнительно медленно – но она работает.

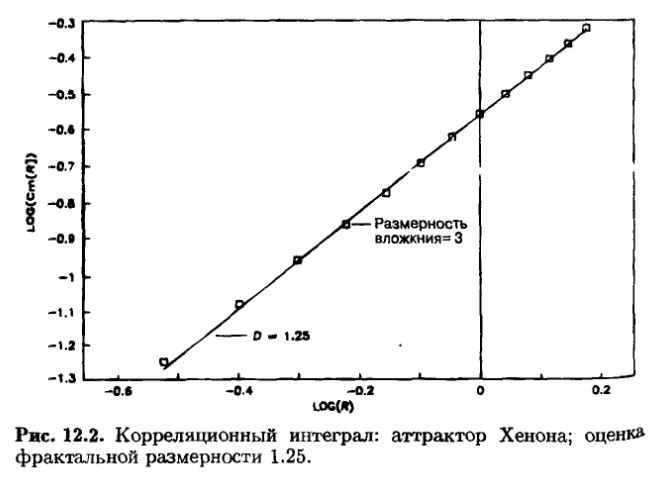
На рис. 12.2 показаны корреляционные интегралы для аттрактора Хенона, полученные с использованием восстановленного фазового пространства по одной переменной способом, рассмотренным выше. График представляет собой зависимость C_m от R в двойных логарифмических координатах для размерности вложения, равной 3. Регрессия представляет собой прямую линию. Оценка D составляет 1.25 против 1.26, полученной при измерении методом оконного скейлинга. Метод Грассбергера и Прокаччи предлагает надежный, относительно простой способ оценки фрактальной размерности в том случае, когда наблюдается только одна динамическая переменная. Этот метод требует обработки большого количества данных и соответственно много машинного времени, однако его результаты отличаются надежностью.