|

Мы рассчитываем фрактальную размерность способом, изложенным в гл. 12. Во-первых, в соответствии с уравнением (12.2) рассчитываются корреляционные интегралы для последовательного увеличивающихся размерностей вложения. При этом просматриваются регрессии на линейных областях двойных логарифмических кривых. Фрактальная размерность должна в конце концов сходиться к своей истинной величине, по мере того как будет увеличиваться размерность вложения.
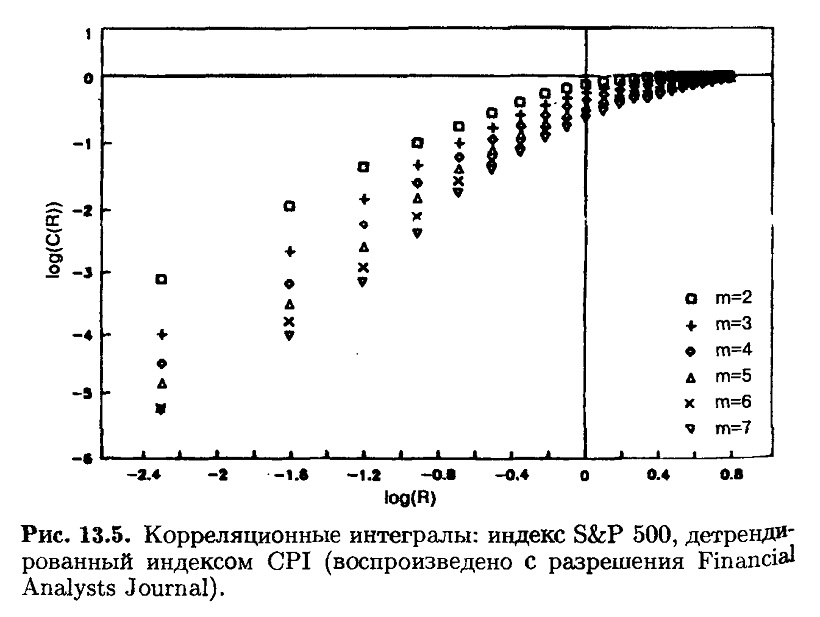
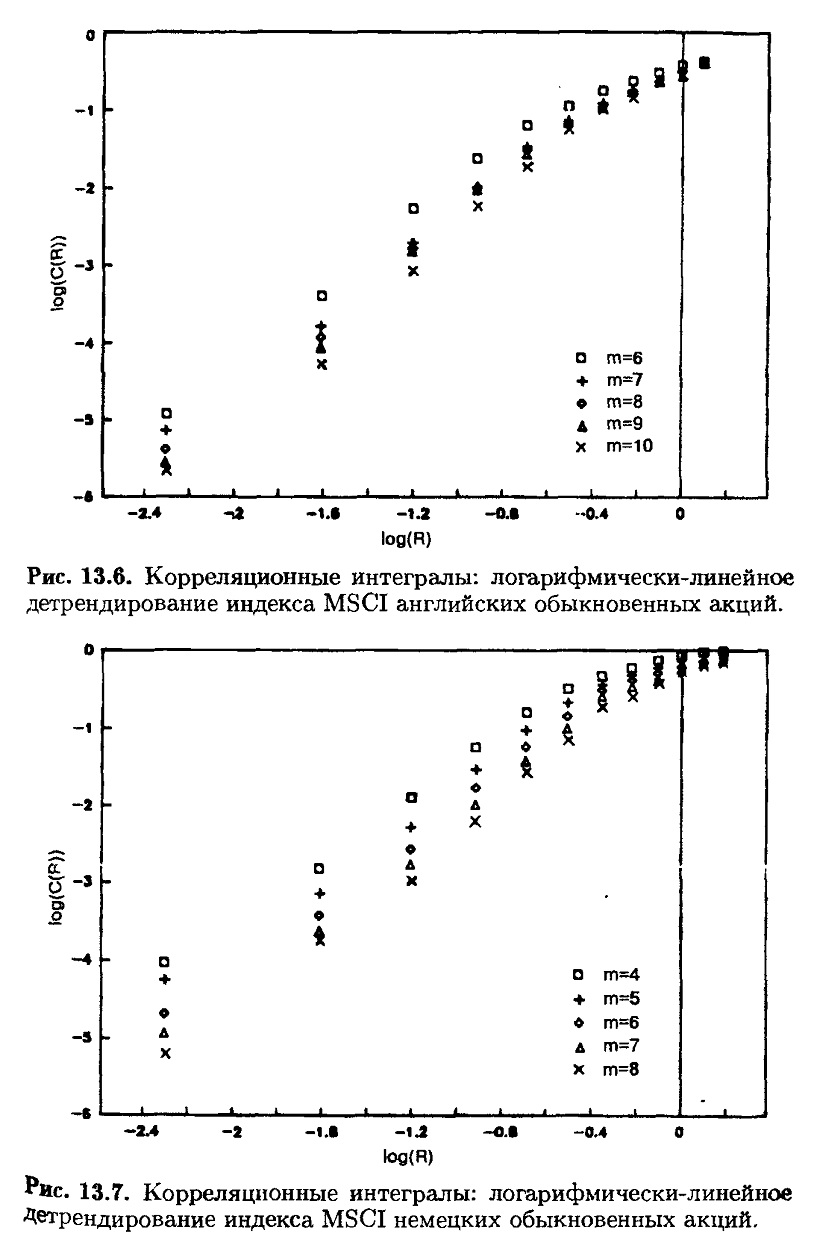
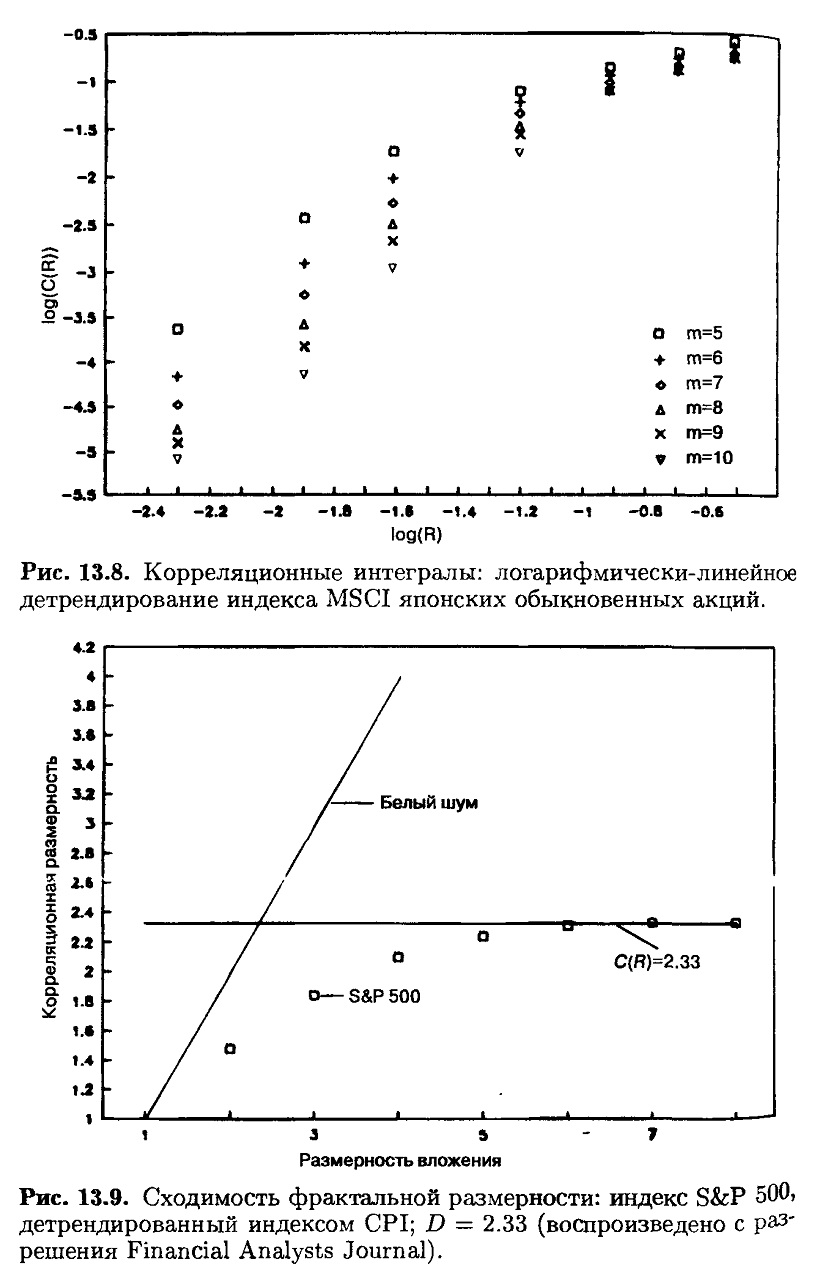
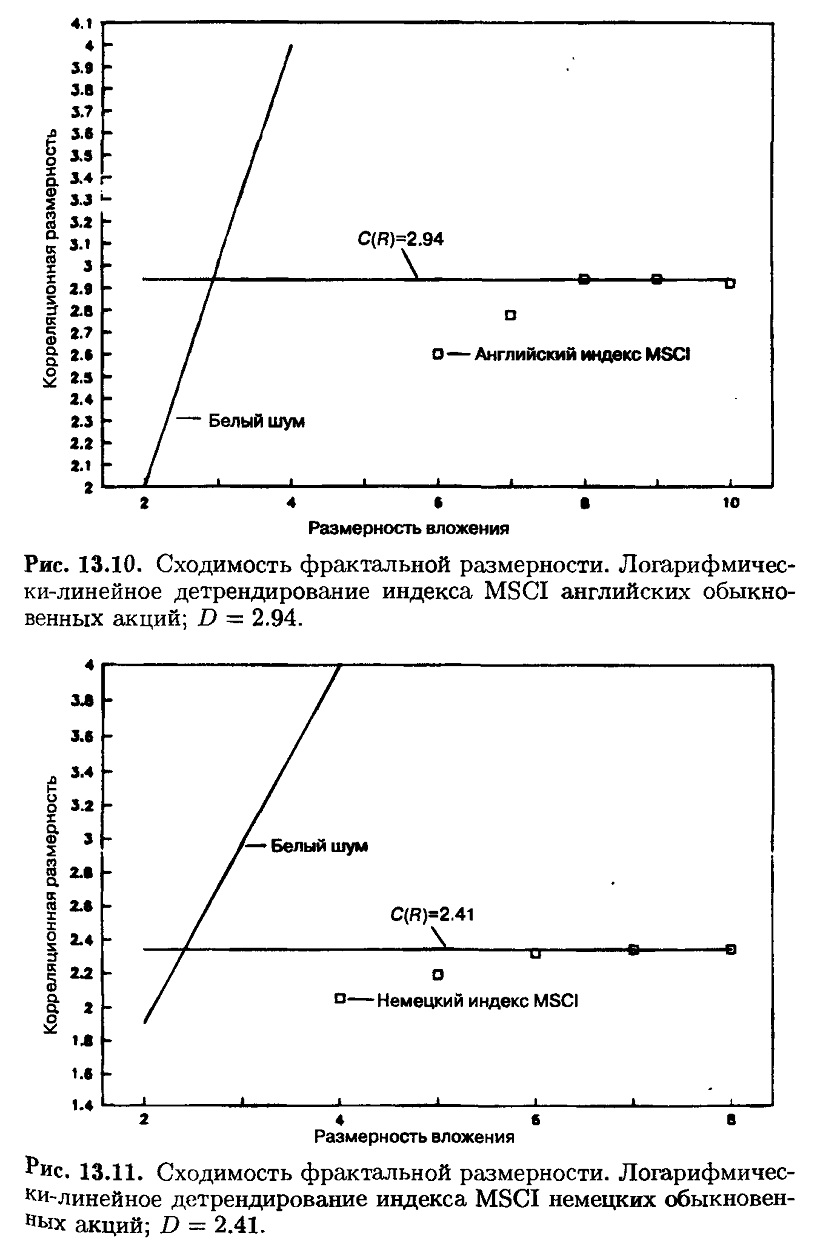
На рис. 13.5-13.8 показаны диаграммы корреляционных интегралов для четырех рынков. Линейные области на каждой диаграмме могут быть использованы для построения регрессий. На рис. 13.9-13.12 показана сходимость к фрактальной размерности. В табл. 13.1 дана сводка результатов.
США, Англия и Германия имеют фрактальную размерность между 2 и 3. Это хорошая новость, потому что это означает, что есть возможность смоделировать динамику этих рынков с помощью трех переменных. Мы не знаем, каковы эти три переменные, но графическое изображение трех переменных представляет собой решаемую проблему.
Для Японии мы видим другую картину. Ее фрактальная размерность равна 3.05, и это означает, что необходимы четыре переменные. Японский рынок более сложен, чем три других рассмотренных рынка.
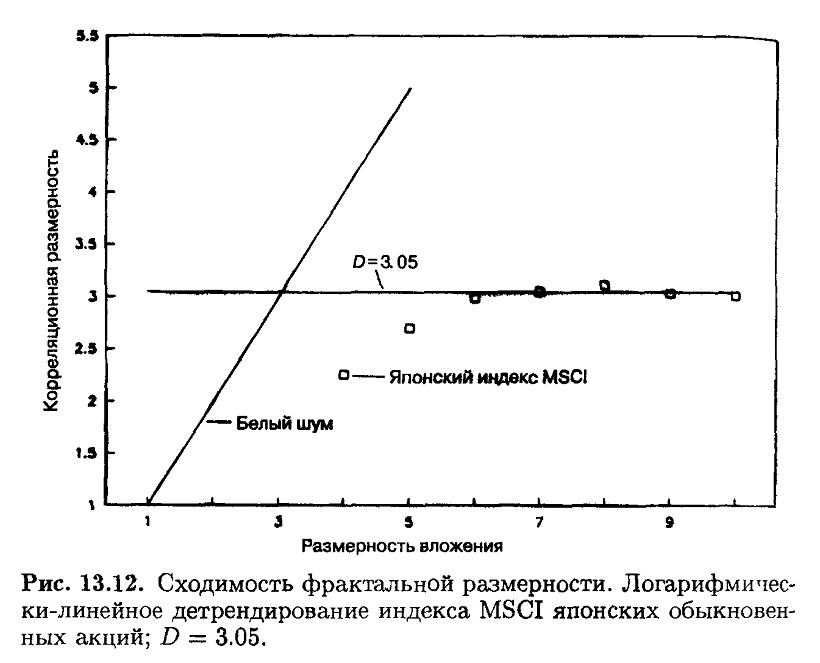
Такая высокая фрактальная размерность говорит также о том, что для анализа требуется больше данных – скорее 1000 точек нежели 500. Однако мы увидим далее, что это не так.
Этот реальный анализ показывает, что устойчивая сходимость к фрактальной размерности согласуется с теорией. Он выглядит обнадеживающе, поскольку, за исключением Японии, системы являются низкоразмерными. А раз так, то они разрешимы, и мы можем надеяться, что они будут решены в недалеком будущем.

|