Показатели Ляпунова

Вычисление показателей Ляпунова требует больших затрат времени. Теоретически показатели Ляпунова остаются постоянными, независимо от того, какие параметры выбираются для их измерения. Увы, реальная жизнь вносит некоторую неясность в эту проблему. Экономический временной ряд включает в себя все фазы системы, а не только хаотические. Наши параметры должны выбираться для максимизации измерения «растяжения» точек в фазовом пространстве и в то же время минимизации «складывания», или ограничений, которые могут иметь место, когда рыночная активность действительно случайна или когда она низка.

«Правило большого пальца», предложенное Уолфом – это всего лишь предложение. Действительные результаты зависят от большого количества численных экспериментов с различными пробными параметрами. Как бы ненаучно это ни звучало, но это так. Плодотворной областью исследований могло бы стать развитие метода, менее подверженного эксперименту, связанному с «раскапыванием данных», т. е. поисками таких данных, которые будут признаны удачными. К счастью, эффекты некорректного описания легко можно увидеть и поправить, но это длительный процесс.

Программа, описанная в Приложении 5, распечатывает результаты каждой итерации. Посредством их изучения можно увидеть, когда особая точка во времени становится причиной отказа этого метода.

Для данных S&P 500 существование двух «долей» во втором и четвертом квадрантах (см. рис. 13.16) порождает особые проблемы в отношении точек замены. Алгоритм Уолфа работает, начиная с двух близлежащих точек в фазовом пространстве (отстоящих одна от другой по крайней мере на один орбитальный период) и следуя их эволюции во времени. Если эти точки слишком сильно отдаляются друг от друга, то ищется точка замены с целью исключения складки. Наибольшие показатели Ляпунова измеряют растяжение, или разбегание точек в фазовом пространстве, но не сходимость. Если одна или две точки попадут в одну долю, то при расчете показателя Ляпунова последует значительное увеличение объема вычислений.

Конечный результат связан с количеством точек данных. Иметь больше точек на коротком временном периоде не всегда лучше, чем иметь меньше данных для большого временного периода. В противоположность статистическому анализу, иметь четырехгодичные ежедневные данные (приблизительно 1000 точек) не лучше, чем 40-годовые месячные данные, или 480 точек. Как мы увидим, при анализе хаоса больший объем данных не всегда с необходимостью предпочтителен.

Возьмем, например, природную систему, подобную хорошо задокументированным солнечным пятнам с циклом 11 лет. Показатель Ляпунова может быть аппроксимирован как 1/11 или 0.09 бит в год. Если мы увеличим разрешение до 11-годовых дневных данных, или 3872 дней, показатель Ляпунова будет 1/38726, или 0.00002 бит в день. В любом случае заявлен 11-годовой цикл. Увеличение количества данных на цикл увеличивает время, потребное для расчета, без повышения точности результата.

Дополнительной проблемой при анализе временных рядов, особенно в случае прибылей на рынках капитала, является шум. При более высоком разрешении, таком, как дневные прибыли, мы обычно находимся в положении, когда имеется больше случайных флуктуаций, чем при низком разрешении. Можно понять, почему исследование Шейнкмана и ЛеБарона дало странные результаты. Оно содержит только пять циклов данных с высоким разрешением, тогда, как мы видели из R/S-анализа, существует высокий уровень шума и/или марковские короткопериодные зависимости.

Такой подход к данным совершенно отличается от того, который принят большинством статистиков. В стандартной статистической теории, чем больше имеется данных точек, тем лучше, потому что наблюдения предполагаются независимыми. Нелинейные динамические системы характеризуются процессами с долговременной памятью – лучше больше времени, чем больше данных. Уолф предлагает и другое правило большого пальца: необходимо примерно 10 циклов.

В главе 9 при использовании R/S-анализа мы нашли, что данные S&H 500 имеют длинный цикл памяти – около 4 лет. Такая длина цикла была очевидна для всех временных приращений прибылей, что сделало ее независимой от разрешения данных. Мы также нашли, что показатель Херста для дневных прибылей равен 0.60, и что он растет при увеличении временных приращений прибылей и стабилизируется на 0.80 для 30-дневных прибылей и выше. Из этой информации мы можем понять, что дневные данные более зашумлены, чем данные месячные, поскольку показатель Херста для них достаточно низок. Месячные и более высокие приращения данных удалили шум, на что указывает их устойчивый показатель Херста. Эффект структуры долговременной памяти также стабилизируется по достижении месячных приращений. Поскольку мы имеем четырехгодичный цикл, то для того чтобы вычислить показатель Ляпунова следует использовать данные за сорок лет.

В итоге мы должны решить, какое разрешение является предпочтительным. Должны ли мы использовать месячные, квартальные или полугодовые данные? Уменьшение разрешения уменьшает потребность в компьютерном времени, но может не дать достаточно данных точек для нахождения точек замены. Здесь должен быть соблюден баланс. К сожалению, такой баланс достигается только путем проб и ошибок.

При оценке S&H 500 месячные данные обладают наинизшим разрешением и наибольшим количеством кандидатур на замены. Применение уравнения (12.4) к нашему детрендированному временному ряду S&H 500 в итоге требует выбора размерности вложения восстановленного фазового пространства, времени эволюции и величины максимального разбегания точек перед заменой.

Как мы упоминали в гл. 12, для выполнения окончательного анализа Уолф дает дополнительные правила большого пальца. Во-первых, размерность вложения должна быть выше, чем фрактальная размерность, потому что грубая поверхность выглядит более гладкой, когда помещена в более высокой размерности вложения. Мы нашли также, что фрактальная размерность S&P 500 равна 2.33, значит размерность вложения должна быть равна 3 или выше. Временной лаг может быть вычислен по уравнению (12.1). Поскольку мы имеем цикл около 40 месяцев, размерность вложения должна бы требовать временного лага равного 16 месяцам. Максимальная длина роста между двумя точками должна составлять не больше 10% протяженности аттрактора. Наконец, время эволюции должно быть достаточным для измерения растяжения без складок.

При выполнении вычислений должна иметь место сходимость к устойчивой величине наибольшего показателя Ляпунова L₁. Если сходимости нет, то или требуется другое описание или система не хаотична.

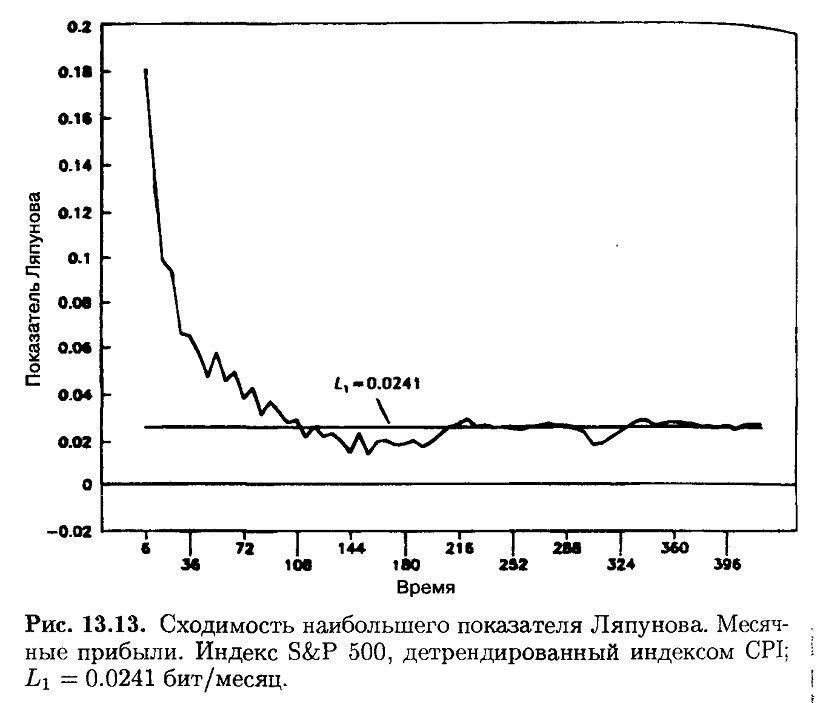
Устойчивая сходимость была найдена для детрендированного ряда данных S&P 500 (месячные данные с января 1950 по июль 1990 гг.) с использованием размерности вложения равной 4, временного лага 12 месяцев и времени эволюции в шесть месяцев. На рис. 13.13 показана устойчивая сходимость показателя L₁ к величине 0.0241 бит/месяц.

Это означает, что мы теряем предсказательную мощность со скоростью 0.0241 бит/месяц. Если бы мы знали точно, какова будет прибыль следующего месяца (т. е. могли бы измерить начальные условия с точностью до одного бита), то потеряли бы всю предсказательную мощность после 1/0.0241, или 42 месяцев. Этот цикл в 42 месяца приблизительно равен 1000-дневному торговому циклу, полученному в гл. 8 с использованием R/S-анализа и подтверждающему, что длина цикла для S&P 500 равна приблизительно четырем годам.

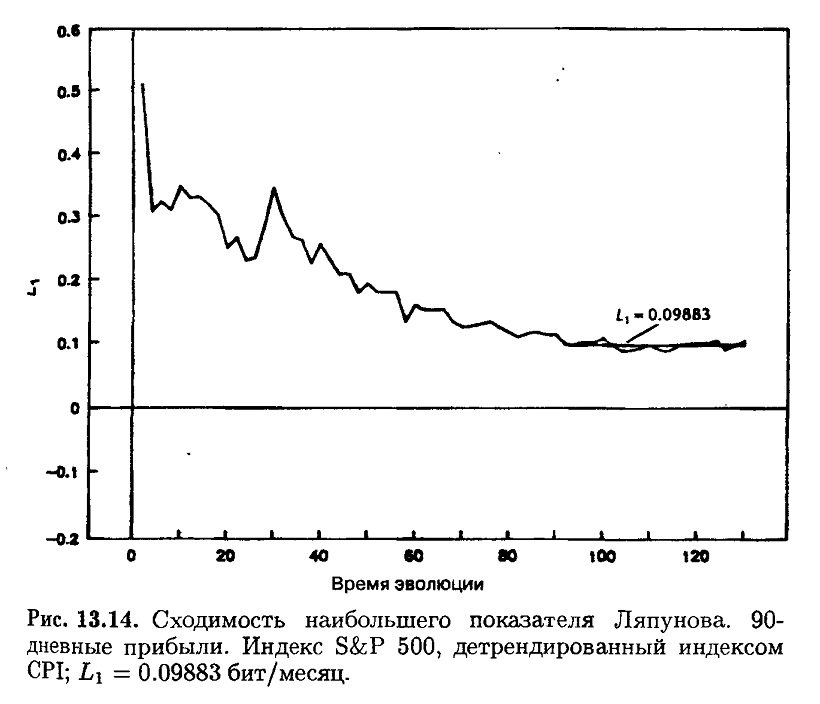
В качестве дополнительного теста я вычислил показатель Ляпунова для 90-дневных торговых данных, использованных в гл. 9 и детрендированных для внутреннего роста по уравнению (13.1). Эти данные охватывают период с января 1928 по июнь 1990 гг., или около 60 лет. На рис. 13.14 показано, что устойчивая сходимость была достигнута при 0.09883 бит на 90-дневный период. Длина цикла снова составила 1/0.09883, или около десяти 90-дневных периодов – приблизительно четыре года.

Тесты по трем международным индексам выглядят обнадеживающе, но при этом не вполне убедительны для Германии. И причиной тому снова недостаточное количество данных. Данные MSCI покрывают период в 41 год, с января 1959 по февраль 1990 гг. Германия, как было найдено из R/S-анализа, имеет цикл длиной около 60 месяцев. Следовательно, наше правило большого пальца говорит, что мы должны иметь примерно 50-летние данные, но у нас их значительно меньше. Япония в точности соответствует этому требованию за период 40 лет, Англия – за 30 лет.

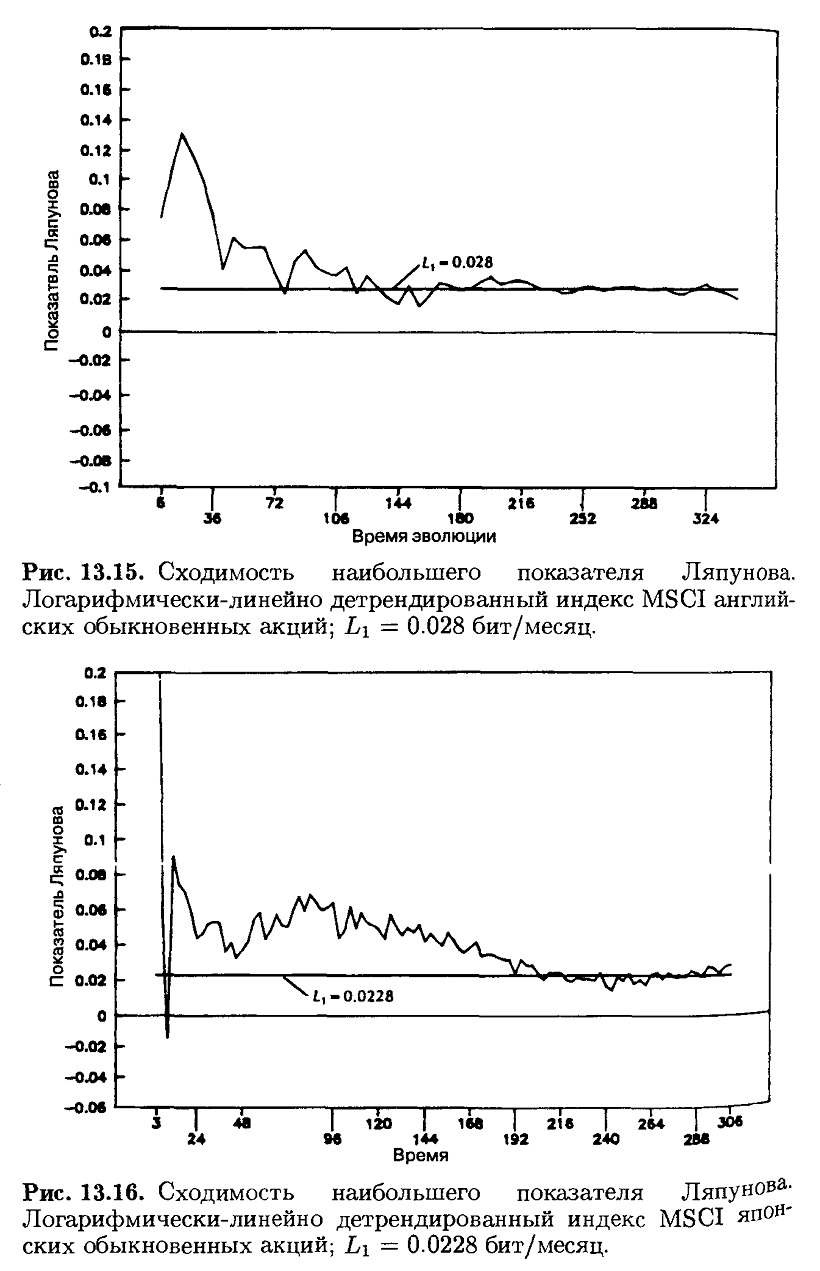
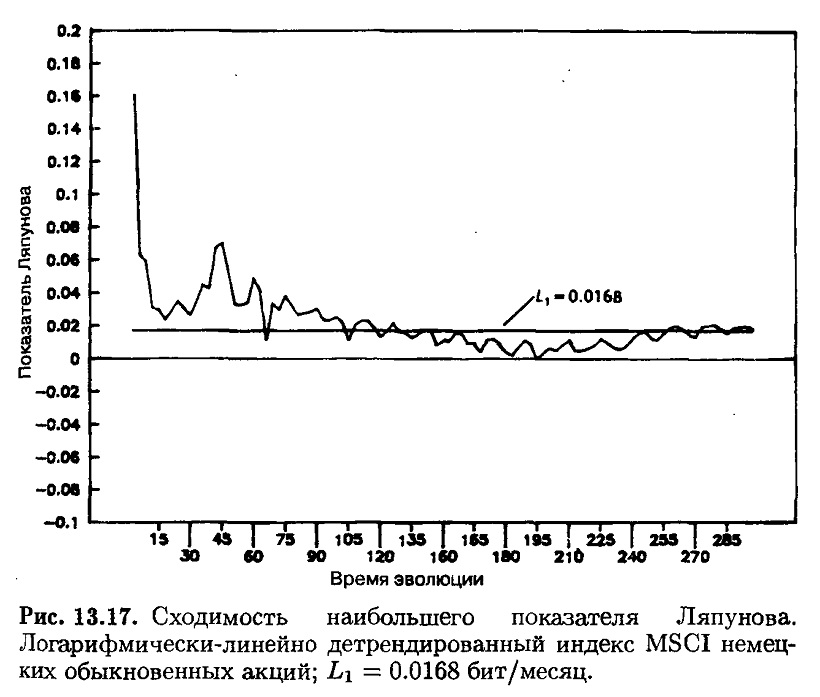
В результате, Англия дает самую гладкую сходимость. Как показано на рис. 13.15, оценка показателя L₁ составляет 0.028 бит/месяц. Инверсия составляет около 36 месяцев. Япония тоже сходится, хотя и более хаотично, к величине L₁ = 0.0228, как это показано на рис. 13.16. И снова инверсия наибольшего показателя Ляпунова подразумевает цикл в 44 месяца, подобный циклу, выведенному с использованием R/S-анализа. Германский рынок дает L₁ = 0.0168 бит/месяц с результирующим временем декорреляции в 60 месяцев. Однако эта величина сходимости, как показано на рис. 13.17, менее убедительна, поскольку для получения устойчивой сходимости требуется больше данных.

Это снова показывает, что когда анализируется такого рода движение, количество точек не так важно, как количество циклов. Мы должны переориентировать наше мышление, когда используем негауссовские данные и методы.

ВЫВОДЫ

Эффект долговременной памяти в ценах на акции теперь подтвержден двумя разными методами нелинейного анализа. R/S-анализ месячных прибылей по данным S&P500 обнаружил смещенные случайные блуждания с длиной памяти около четырех лет. Показатель Ляпунова для месячных инфляционно-детрендированных цен по S&P 500 обнаружил 42-месячный цикл. Подобные же соотношения были найдены для Англии, Японии и Германии с использованием числовых индексов ценных бумаг MSCI.

Показатель Ляпунова может быть интерпретирован двумя способами. В Соединенных Штатах мы теряем предсказательную способность со скоростью 0.0241 бит в месяц. Если бы мы могли измерить начальные условия с точностью до одного бита, то потеряли бы всю предсказательную способность после 42 месяцев. Это «вперед смотрящая» интерпретация из гл. 12. Но это также и «назад смотрящая» интерпретация. Система теряет всю память о начальных условиях после 42 месяцев. В среднем рыночные показатели, отстоящие на 42 месяца или более, не соотносятся и не коррелируют. Эта интерпретация показателя Ляпунова подобна времени декорреляции, или циклу, найденному с помощью R/S-анализа. В последнем переход к поведению случайного блуждания через четыре года означает, что эффект долговременной памяти диссипирует после четырех лет – прибыли становятся независимыми. Такое подобие в концепциях и результатах поистине поразительно.

Важно заметить, что длина цикла непериодична. Среднюю длину такого цикла нельзя обнаружить стандартными методами, подобными спектральному анализу, потому что она не имеет характерного масштаба. Это также не «диаграммный» цикл или цикл «пик – впадина», столь дорогие сердцу технических аналитиков. Это статистический цикл; он измеряет влияние информации на рынок и то, как память о тех или иных событиях влияет на будущее поведение рынков.