|

Формально не существует математической связи между хаотическими системами и фракталами. Тем не менее ее легко проследить на графике возможных решений хаотической системы. Даже одномерная система, подобная логистическому уравнению, демонстрирует свою фрактальность.
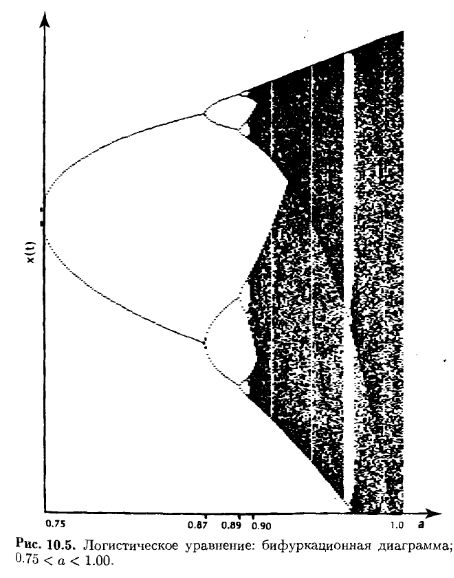
На рис. 10.5 представлена бифуркационная диаграмма логистического уравнения. На график нанесены возможные величины х, соответствующие различным константам а. (Краткое описание бейсик-программы, выполняющей вычисления и рисование графика, дано в Приложении 1.) Из графика видно, что несмотря на хаотичность системы, имеет место определенная упорядоченность в ее возможных решениях. На нижних уровнях а существуют единичные равновесные решения. Видны также точки бифуркаций и область хаоса между значениями а, равными 0.90 и 1.0. Но даже в хаотической области наблюдается некий порядок.
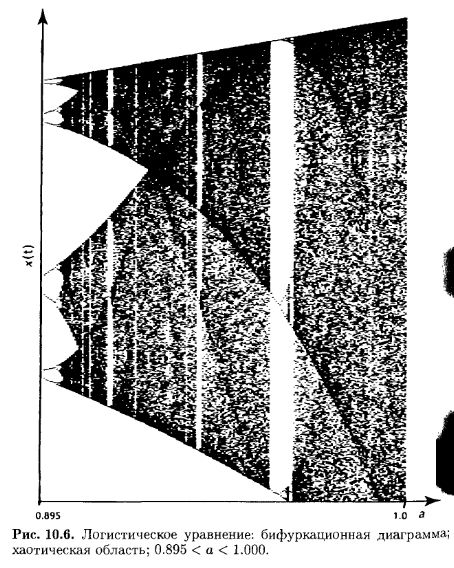
На рис. 10.6 показана бифуркационная диаграмма в диапазоне а от 0.895 до 1 на графике с более высоким разрешением. На этом уровне детализации можно видеть, что хаотическая область не сплошь покрыта точками. Нечто вроде «горных хребтов» повисает вниз подобно вуалям. На них точки сгущается, в то же время их прорезают белые полосы, где, кажется, порядок склонен вернуться в систему, и он действительно снова утверждает себя (а < 0.90).
Эти полосы интересны еще тем, что они иллюстрируют фрактальную природу системы. На рис. 10.7 показана такая белая полоса с увеличением в диапазоне 0.955 < а < 0.966. В этой упорядоченной области мы видим миниатюрные версия целостной бифуркационной диаграммы. Если, в свою очередь, увеличить их, то в них обнаружатся еще меньшие участки, подобные целому, и так до бесконечности. Такого рода самоподобие и образует фрактал, – по определению, данному в гл. 5.
Бифуркационная диаграмма представляет множество возможных решений уравнения. Все точки в хаотической области статистически не равновероятны. Темные полосы и устойчивые в широком диапазоне решения указывают на изменчивость вероятностей при возрастании а. При каждом а в хаотической области имеется бесконечное количество решений, заключенных в конечном пространстве, как в игре хаоса.

Теперь мы можем предположить, что фрактальная статистика рынков капитала, которую мы изучали в части 2, имеет причиной нелинейные динамические системы. Далее мы обратимся к их изучению.
ВЫВОДЫ
Я попытался нарисовать интуитивно улавливаемую связь между миром фракталов и областью нелинейных динамических систем. Высокоразмерные хаотические системы, которые мы будем обсуждать в части 3, имеют много общего с логистическим уравнением, и они также связаны с фракталами.
|