Удаление трендов из данных

В количественном анализе рынков капитала мы всегда используем прибыли; это значит, что мы используем процент изменения в ценах вместо самих цен. Цены не подходят для линейной регрессии, поскольку они последовательно коррелированы. Каждая цена соотносится с ценой предшествующей – в нарушение предположений, необходимых для использования гауссовского линейного анализа. Мы пытаемся предсказывать прибыли, но мы не должны забывать, что объективно это есть предсказание поведения цен. Прибыли просто-напросто делают данные подходящими для линейного анализа и сопутствующих требований о независимости этих данных.

Процентное изменение не может быть пригодным временным рядом для нелинейного динамического анализа системы. Оно отбеливает данные путем исключения последовательной зависимости, которая может проявляться в шуме нелинейной зависимой структуры. Когда ученые изучают турбулентность в естественных системах, фазовое пространство состоит из наблюдаемых данных, а не из скоростей изменения переменных Финансы и экономическая теория имеют давнюю традицию использования прибылей. В изучении рынков как нелинейных динамических систем нам необходимы новые стандарты Прибыли не являются подходящей трансформацией цен при исследовании нелинейных динамических систем.

Предшествующее изучение рынка обыкновенных акций как нелинейной динамической системы было сосредоточено на прибылях. Результаты не были обнадеживающими. Шейнкман и ЛеБарон (Scheincman, LeBaron, 1986) нашли изящную совокупность доказательств нелинейности динамической структуры, включая положительный показатель Ляпунова и фрактальную размерность. Однако они обнаружили, что их ряд дневных прибылей, состоящий из 5000 наблюдений, имеет фрактальную размерность между 5 и 6. Эта фрактальная размерность выглядит обескураживающей, потому что она подразумевает динамическую систему с шестью переменными. Такую систему практически невозможно описать или смоделировать ввиду ее чрезвычайной сложности. Это исследование похвально, тем не менее его результаты остаются под вопросом, так как использование 5000 дневных прибылей не является адекватным самому методу. Как было сказано в гл. 12, потребовалось бы минимум десять миллионов точек данных для системы с фрактальной размерностью такой величины. В сочетании с размерностью вложения, которая была использована Шейнкманом и ЛеБароном для восстановления фазового пространства (т = 14), это множество данных слишком разрежено, для того чтобы дать надежный результат. К тому же, R/S-анализ показал, что значение орбитального периода для американского рынка обыкновенных акций составляет четыре года. Это означает, что для такого анализа были бы необходимы 10 орбитальных периодов, или данные за 40 лет (примерно 10000 дневных прибылей). Названные авторы показали, что использование прибылей радикально осложняет проблему и что альтернативой должен быть анализ, не использующий процентов изменений. По аналогии с естественными науками выглядит разумным использование реальных объектов изучения, а именно цен.

Использование цен влечет за собой разнообразные проблемы. Величина активов растет вместе с экономикой и подвержена инфляции. Цены растут просто по причине одной лишь инфляции, даже если нет реальных перспектив их роста. Цены могут расти бесконечно. Фазовое пространство номинальных цен (т. е. цен без поправок на инфляцию) будет просто взлетающей спиралью. Анализировать такой временной ряд было бы бесполезным занятием.

Следовательно, мы должны детрендировать цены к экономическому росту, поскольку нас интересует именно движение цен, а не их инфляционный рост. Чен (Chen, 1988) детрендировал денежную массу посредством исключения внутренней скорости ее роста. Он нашел, что денежное предложение, измеряемое экономическим индексом Дивижи (Индекс денежного предложения, публикуемый американским федеральным резервным банком) имеет странный аттрактор с фрактальной размерностью 1.24 и длиной цикла в 42 месяца. Эта длина цикла подобна циклу казначейских облигаций, который мы нашли в гл. 9, используя R/S-анализ. Чен детрендирует цены по формуле:

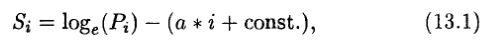
где S_i – детрендированный ряд цен, P_i – исходный ряд цен, i – номер наблюдения.

Посредством регрессии логарифма цены на время и вычитания этих двух рядов мы получаем новый ряд с исключенным трендом экспоненциального роста во времени.

Этот метод привлекателен, однако он предполагает, что экономический рост происходит с постоянной скоростью. Поскольку мы знаем, что это не так, было бы предпочтительным исключить тренд посредством переменной, более непосредственно относящейся к экономическому росту.

Предпочтительной переменной был бы совокупный национальный доход (GNP), но эти данные имеются только поквартально. Нам необходим ряд по меньшей мере месячных Данных. Альтернативой могло бы быть измерение инфляции, Поскольку активы растут вместе с инфляцией. Посредством вычитания инфляции мы можем получить ряд реальных цен и попытаться смоделировать их движение.

Мы можем привести уравнение (13.1) к следующей инфляционно скорректированной форме:

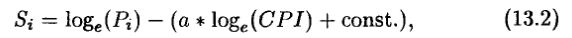
где CPI – индекс цен на потребительские товары. В Соединенных Штатах информация о потребительских ценах фиксируется в течение многих лет. В других странах это не так. Поэтому мы будем использовать уравнение (13.2), когда данные об инфляции доступны, и уравнение (13.1) в противном случае.

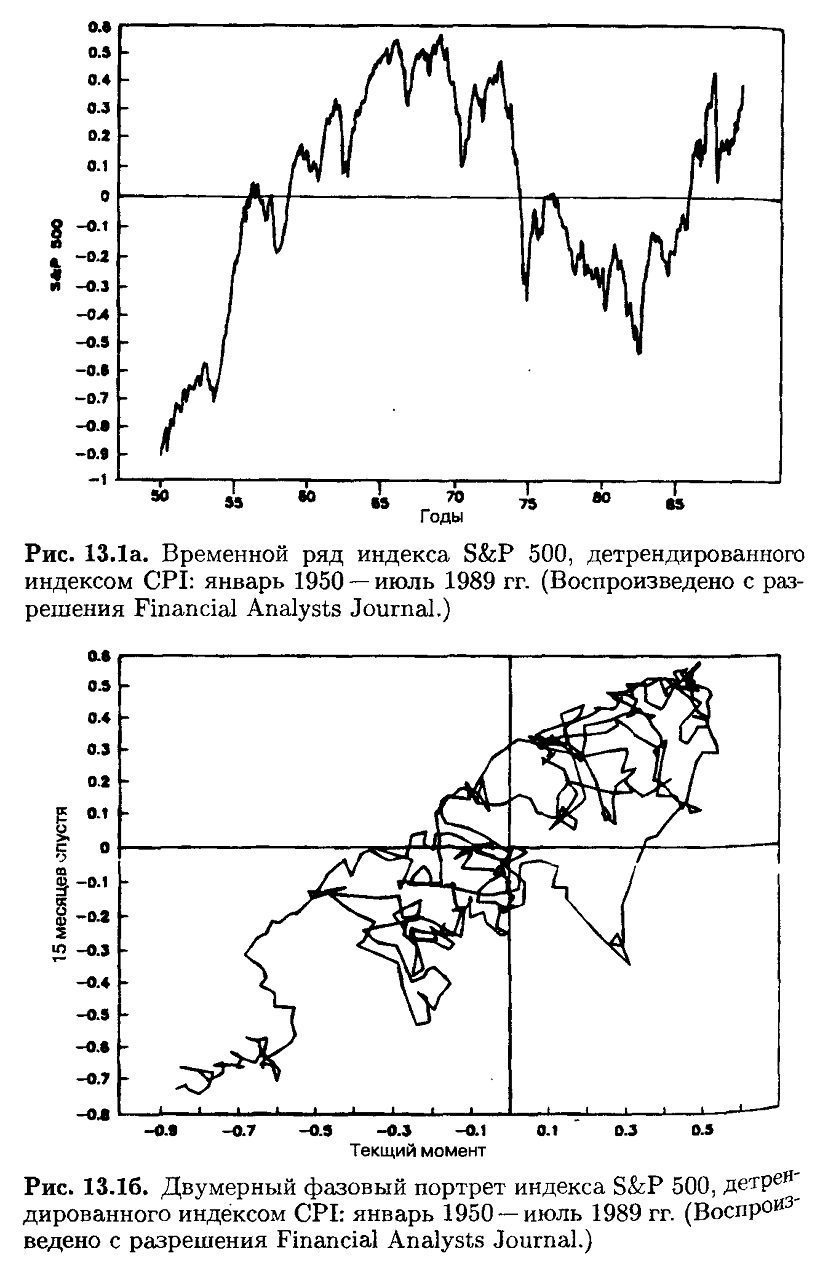
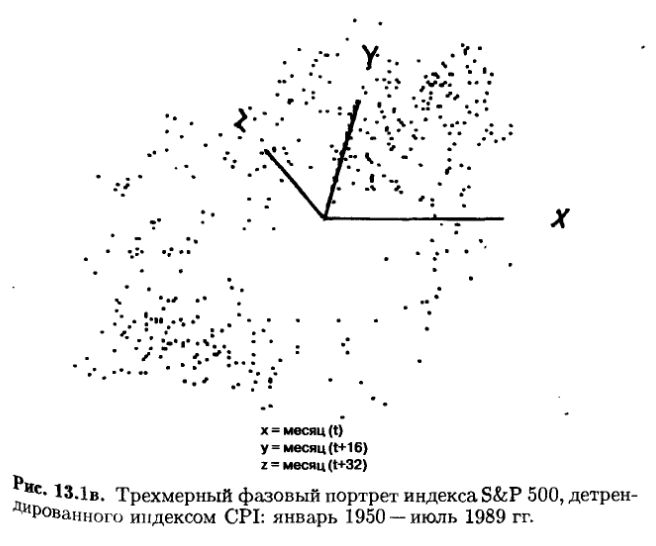
Детрендированные данные S&P 500 с января 1950 по июль 1989 гг. показаны на рис. 13.1а. Этот ряд имеет волнообразный характер. В ценах проявляется периодичность, когда они остаются высокими, инфляционно скорректированными или низкими. Двумерное фазовое пространство показано на рис. 13.16. Временной лаг –15 месяцев. При вычерчивании графика движение идет по часовой стрелке, подобно спиральному хаосу. Траектория делится на (или имеет) две доли. Одна заключена во втором квадранте и содержит периоды, когда рыночные цены ниже, чем их инфляционно скорректированные величины. Вторая доля заключена в четвертом квадранте и соответствует низкоинфляционному тренду. Эти две области связаны рукавом, который отражает переход из одной доли в другую. На рис. 13.1в представлено трехмерное фазовое пространство с временным лагом 16 месяцев. Основная структура сохраняется – два бассейна притяжения, связанные рукавом.

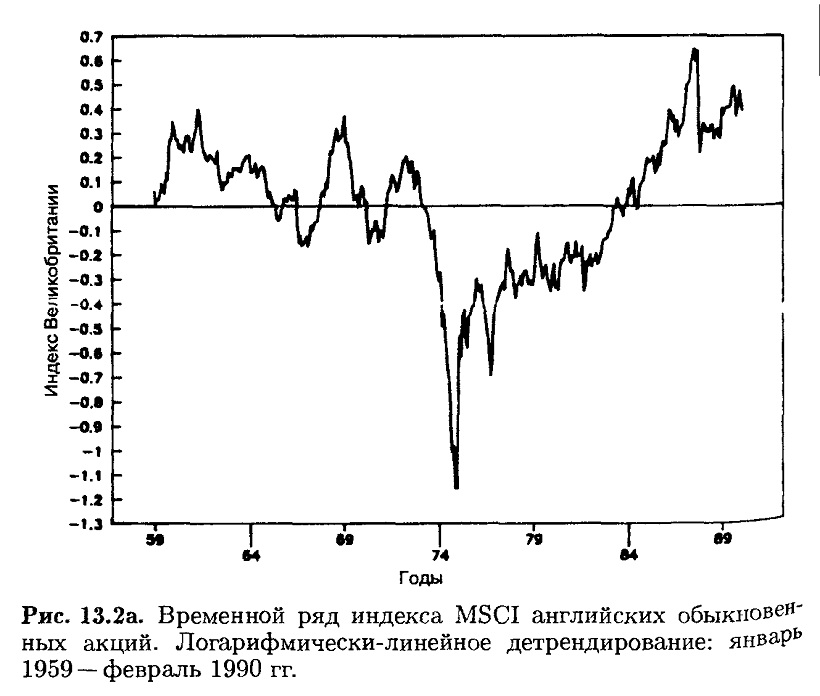
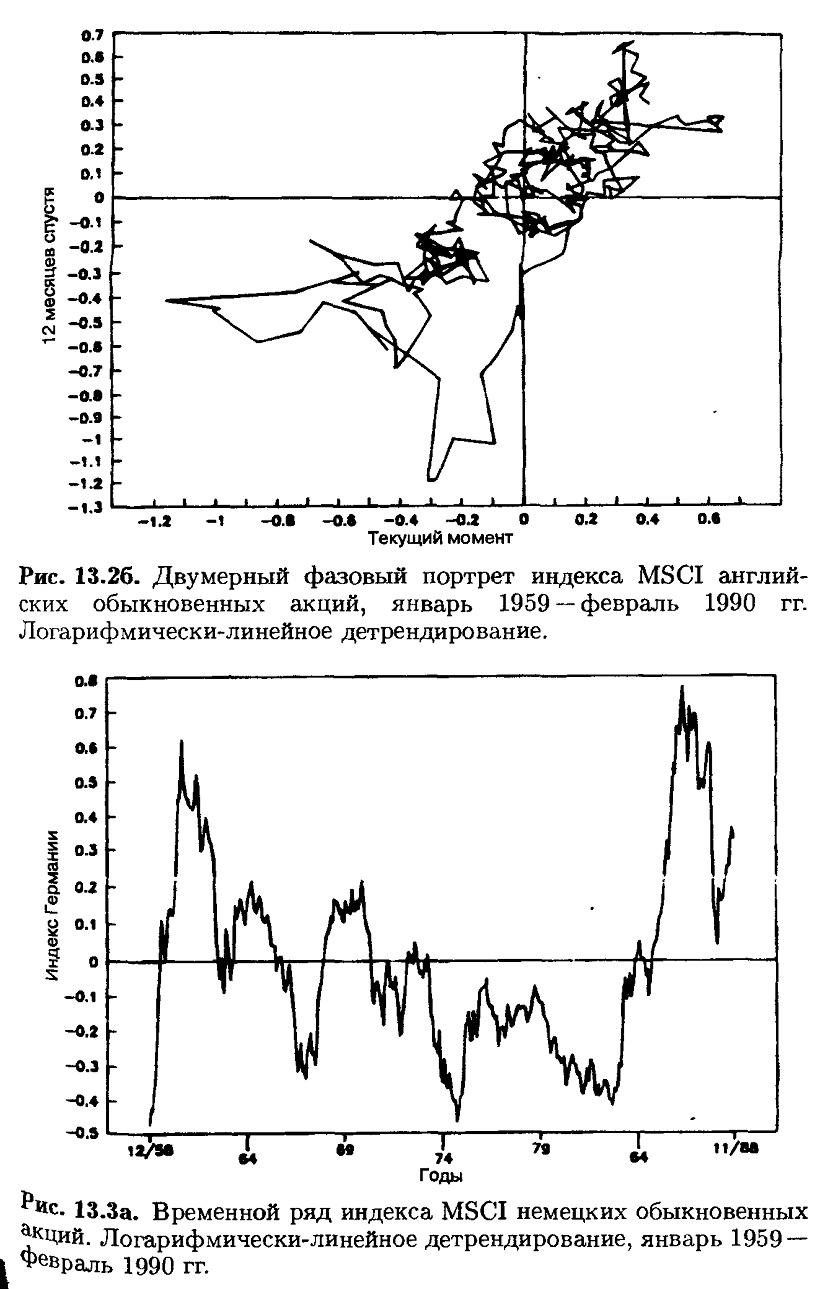
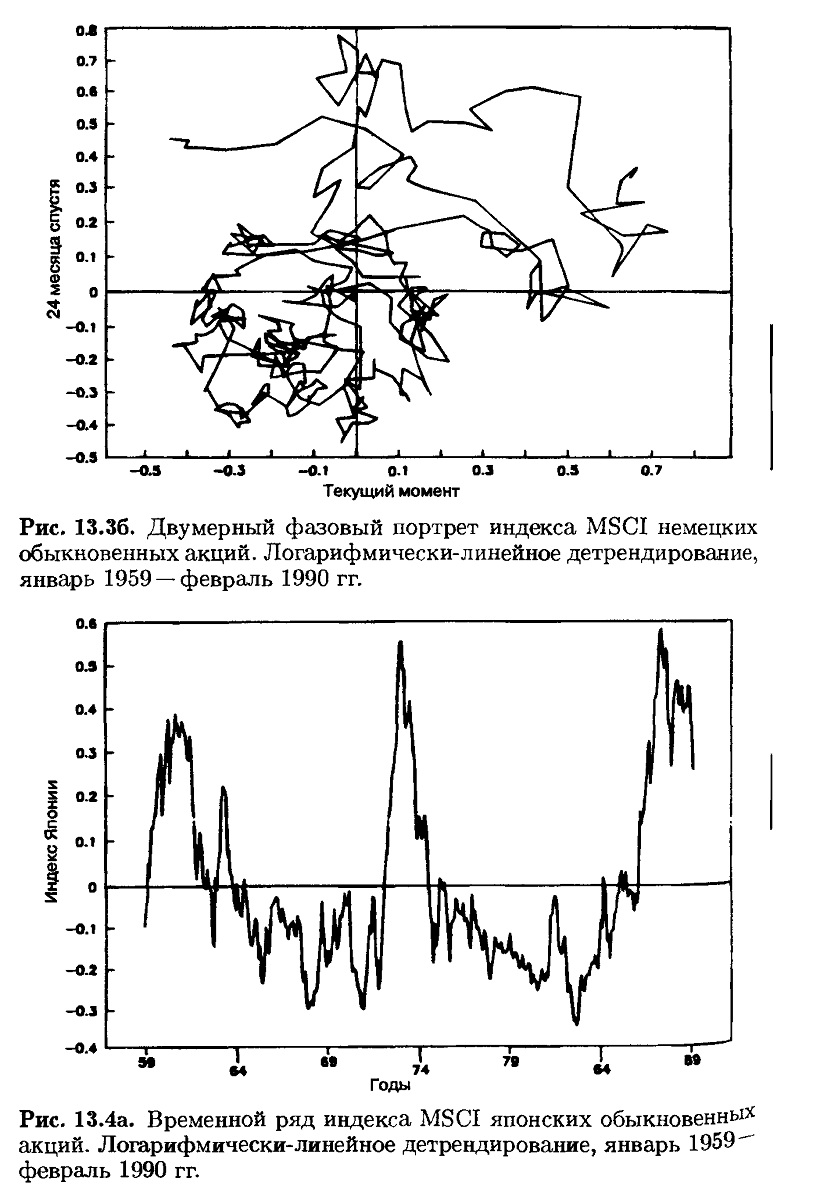
На рис. 13.2-13.4 продолжен такого рода анализ в отношении британского, германского и японского рынков с исключением трендов – корректировкой на экономический рост (показатели инфляции недоступны). Был использован индекс международного капитала Моргана – Стенли (MSCI) за период с января 1959 по февраль 1990 гг. в собственной валюте. Каждая страна обладает собственной динамикой, графики вычерчиваются по часовой стрелке. Британский рынок был под влиянием большого падения в начале 1970-х годов, когда британская экономика переживала спад и фунт стерлингов потерял свои позиции. Вне этого периода британский рынок претерпевал колебания относительно своей внутренней скорости роста. Германский рынок демонстрирует замечательную стабильность на протяжении всего периода.

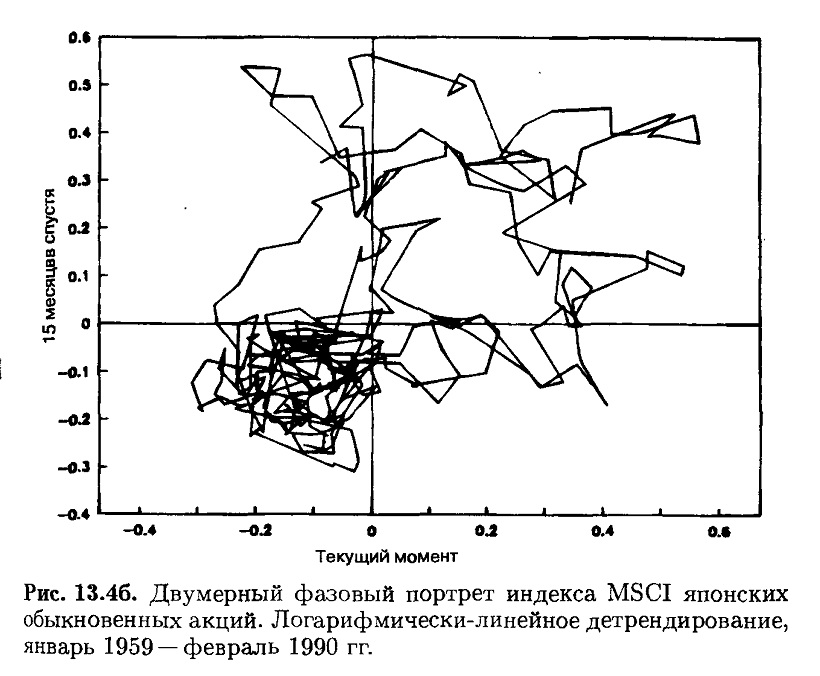
Японский рынок имеет периоды устойчивого роста, следующие за ускоренным возрастанием стоимости запасов и последующих резких падений со стабилизацией состояния. Такая картина наблюдалась в конце 50-х, конце 60-х и с середины до конца 80-х годов. Подобным образом в 1990 г. фаза гиперроста снова продемонстрировала самокоррекцию.

Эти восстановленные фазовые пространства не являются «техническими» графиками, относящимися к техническому анализу (точки, диаграммы и т. п.). Они являются базовыми Данными для нахождения характеристик, необходимых для определения рынков как нелинейных динамических систем. Мы можем использовать теперь эти детрендированные данные для восстановления фазовых пространств, расчета фрактальных размерностей и показателей Ляпунова.