|

Нечеткая логика исходит из того, что люди классифицируют предметы в определенном порядке, чтобы их познать. Подобным образом они классифицируют ситуации в соответствии со своим прошлым опытом с целью принятия решений. Начиная с XIX века предполагалось, что люди должны принимать рациональные решения. Это означает, что для каждого возможного исхода мы должны оценивать его вероятность. К несчастью, возможности нашего мозга слишком ограничены, чтобы достигать столь идеальной рациональности мышления. Вот почему было столько восхищения, когда был создан компьютер. Появилась машина, которая могла рассчитывать «рациональную» оценку ситуации при наличии достаточного количества информации. Предполагалось, что это будет истинная оценка даже при использовании первых компьютеров, предназначавшихся для решения весьма ограниченного круга проблем.
Вначале компьютеры были применены для игры в шахматы. До того, как были развиты методы искусственного интеллекта (ИИ), компьютеры рассматривали все возможности и выбирали наилучший вариант на основании статистических предположений. Поскольку люди не могут рассчитывать все возможные комбинации (оценку вероятности успеха оставим в стороне), предполагалось, что ни один человек не может превзойти компьютер в шахматной игре. Тем не менее, ни один компьютер, использующий этот метод «грубой силы», не смог достигнуть уровня гроссмейстера. Живые гроссмейстеры всегда побеждали. При том, что гроссмейстер не располагал даже той небольшой компьютерной вычислительной мощностью, он имел другие способности. Гроссмейстеры играли сами и изучали тысячи игр. Играя, они, как правило, обнаруживали подобие между текущей стадией своей игры и другими известными им партиями. Конечно, другие партии не могли быть идентичными текущей, но они могли быть достаточно похожи для того, чтобы чему-то научиться. Это ограничивало «поиск» игр с благоприятными окончаниями. Посредством применения их стратегий к своей игре гроссмейстер мог правильно выбрать ходы. Компьютерные программы «грубой силы» не могут учиться у прошлого и адаптироваться. Таким образом, они всегда остаются в невыгодном положении.
Гроссмейстеры используют опыт прошлого, чтобы принять решение. Заметим, что они не копируют прошлое. Вместо того они используют свои знания для классификации ситуации, в которой, например, атака выглядит предпочтительнее обороны. Затем они формулируют точную стратегию собственной игры. В этом процессе классификации и установления подобия содержится то, что составляет сердцевину нечеткой логики.
Название нечеткая логика не совсем точно. Существует некоторая область, именуемая «нечеткая логика», которая имеет дело с многочисленными формами логики. Мы не будем заниматься здесь всей этой областью. Нечеткая логика будет обозначать здесь широкий диапазон приложений теории нечетких множеств. Нечеткие множества и есть то, о чем в большинстве думают как о нечеткой логике.
Нечеткие множества имеют дело с проблемами классификации. Однако перед тем как заняться нечеткими множествами мы должны бросить взгляд на классическую или четкую теорию множеств.
Классическая теория множеств, подобно классической геометрии, была сформулирована древними греками и также восходит к Платону. Множество есть совокупность объектов. В четких множествах отдельный объект или принадлежит множеству, или нет. Это значит, что кокер-спаниель принадлежит множеству всех собак, в то время как персидская кошка – нет. Два разных множества могут иметь общие объяты. Они являются пересечением двух множеств. Например, пересечением множества всех любимых животных и множества всех рыб были бы все любимые рыбы, скажем гуппи. Объединение двух множеств есть все объекты, сложенные вместе. В нашем примере это были бы все любимые животные и все рыбы.
Дополнение множества есть множество всех объектов, не принадлежащих множеству. Так, дополнением множества всех животных, которые являются любимыми, было бы множество всех нелюбимых животных. По определению, пересечение четкого множества и его дополнения есть пустое множество. Такого пересечения не существует. Это называется законом противоречия. Животное не может быть одновременно любимым и нелюбимым. Объединение множества и его дополнения есть универсум. Таким образом, дополнением множества всех любимых и множества всех нелюбимых животных является множество всех животных. Это называется законом исключенного третьего. Это значит, что животное должно быть или любимым или нелюбимым.
Парадокс
Для простых множеств эти определения работают прекрасно. Мы можем с определенностью провести грань между животными любимыми и нелюбимыми. Однако такое использование жестких определений может приводить к проблемам, которые называются парадоксами. Возьмем пример, который носит название парадокс кучи.
Начните с кучи песка. Переместите одну песчинку слева направо – у вас останется куча. Переместите другую песчинку, и еще одну. В конце концов, у вас останется слева одна песчинка. Это все еще куча? Если нет, то когда она перестала ею быть?
Вот где появляется суть нечетких множеств. Две песчинки – это куча? А одна? Возьмем другой пример. Предположим, что имеется множество высоких людей. Как мы определим такое множество? Кто-либо шести футов роста считается высоким? Тогда как насчет пяти футов одиннадцати дюймов? Если это высокий рост, то что можно сказать о пяти футах десяти дюймах? Когда мы решаем, что кто-то высокий, а кто-то нет? Где мы применяем закон исключенного третьего?
Для четких множеств мы должны установить пределы Следует решить, что люди шести футов роста или выше являются «высокими». Индивиды ниже этого роста принадлежат дополнительному множеству «невысоких». Так, кто-либо пяти футов одиннадцати дюймов – невысок. Но это выглядит неразумным. Как может один дюйм составить разницу между высоким и невысоким? Определенно, когда мы видим кого-то, кто обладает ростом пять футов одиннадцать дюймов, мы не можем классифицировать его как человека невысокого. Он высок, но не очень. В этом состоит затруднение. Понятие высоты очень сложно для того, чтобы оперировать с четкими множествами. Решение о том, что кто-то высок в большей степени, зависит от точки зрения. Мы, несомненно, можем распространить это и на более важные понятия, такие, как справедливость и несправедливость, точность и неточность. Даже в военных действиях – что есть война и что не война? Формально Вьетнам и Корея не были войнами, поскольку не было объявления войны. Однако для людей, которые воевали, это определенно были войны.
Четкие множества не могут оперировать с такими понятиями. Они слишком сложны. Лотфи Заде (Lotfi Zadeh, 1965) ввел понятие нечетких множеств, чтобы приспособить теорию множеств для сложных ситуаций. Надобность нечетких множеств была установлена в его законе несовместимости, который был пересказан МакНейлом и Фрейбергом (McNeill, Freiberger, 1994) следующим образом:
«С возрастанием сложности точные утверждения становятся менее осмысленными, а осмысленные утверждения теряют точность».
Таким образом, перед лицом сложных ситуаций требования точности четких множеств становятся непродуктивными. В частности, закон исключенного третьего и закон противоречия слишком точны для использования. В языке мы крутимся вокруг этих проблем, используя «лазейки», такие, как почти, вокруг, около. Мы также используем «определения» вроде зеленый, большой, быстрый.
Заде развил теорию множеств путем обобщения понятия множества. В четких множествах объект находится или внутри множества, или вне его. В бинарном представлении такой объект равен нулю или единице. Заде ввел частичную принадлежность множеству, описываемую функцией принадлежности. Функция принадлежности определяет, насколько подобен объект данному множеству. В четких множествах функция принадлежности равна или нулю, или единице. Это или полное подобие множеству, или полное отличие от него. В нечетком множестве функция принадлежности может находиться в диапазоне между нулем и единицей и включать все дробные величины этого промежутка. Так, человек шести футов роста имеет функцию принадлежности, равную единице в множестве высоких людей, в то время как некто пяти футов одиннадцати дюймов может иметь функцию принадлежности 0.9, а некто пяти футов четырех дюймов – функцию принадлежности 0.1. Теория множеств была обобщена, и внезапно исчезли все парадоксы. Теперь мы можем строго определить туманные понятия, такие, как например «куча». Груда в 1000 песчинок имеет функцию принадлежности 1.0 к множеству «куча». Груда в 20 песчинок имеет функцию принадлежности 0.4. Как это было в случае с фракталами, обобщение теории с включением дробных величин размерности увеличивает ее полезность и укрепляет связи с реальностью.
Нечеткие множества
Как мы установили, нечеткое множество является способом описания сложных понятий. Чем больше становится их сложность, тем более нечеткими становятся сами понятия. Например, множество целых чисел от 1 до 10 есть простое четкое множество. Однако предположим, что множество составляют «целые числа около шести». Пять около шести. Так же и семь, и восемь. Но что сказать относительно 11 или 16? Нечеткие множества дают нам точный способ определения этого понятия – «около 6», но он субъективен. Графически это можно представить так, как сделано на рис. 15.1.
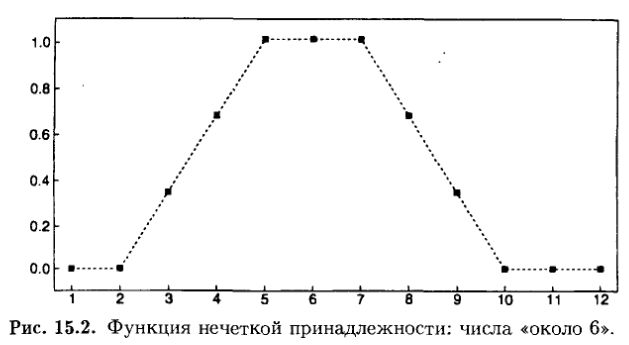
В четком множестве мы должны были бы решить точно, что означает «около 6». Если мы решим, что числа от 5 до 7 – «около 6», мы получим рис. 15.2. На нем показано подобие чисел понятию «около 6». По оси у располагаются функции принадлежности. Как можно видеть, в терминах обычного четкого множества величины, меньшие 5 или большие 7 получают величину функции принадлежности, равную 0. Они не «около 6». Только числа 5, 6 и 7 – «около 6», и, будучи таковыми, они все равны между собой. В нечетком множестве мы должны решить вопрос относительно того, являются ли числа определенно не «около 6» и каковы функции принадлежности каждого числа. В данном примере мы установим, что число, меньшее 2 или большее 10, – определенно не около 6. Величины от 5 до 7 – определенно около 6 и, следовательно, имеют функцию принадлежности, равную 1. В диапазоне от 2 до 5 проводим прямую линию от у = 0 до у = 1. От 7 До 10 также проводим прямую с отрицательным наклоном от у = 1 до у = 0. Величины ординат этих прямых соответствуют функциям принадлежности чисел, расположенных по оси абсцисс, к множеству «числа около 6». Таким образом, число 4 имеет величину функции принадлежности 0.67, а число 5 – величину функции принадлежности 1. Пять в большей степени «около 6», чем 4, но 4 остается «около 6». Мы могли бы получить границы множества, подобные форме функции принадлежности, различными способами. Как мы делаем выбор? Вот в чем состоит сила и слабость нечетких множеств. Параметры такого выбора субъективно зависят от природы проблемы. Адекватность модели зависит от того, как хорошо создатель модели понимает проблему. Хорошее понимание проблемы даст в результате хорошую нечеткую модель. Однако модель, разработанная при ошибочном понимании проблемы, даст результаты со всеми теми ограничениями и ошибками, которые может сделать моделирующий.
Кроме того, существуют различные определения для дополнения, объединения и пересечения нечетких множеств. Они подобны правилам для четких множеств. Мы дадим здесь основные определения; обобщенные определения могут быть изучены более подробно по книге Заде и Каспржик (Zadeh, Kacprzyk, 1992):

Как можно видеть, дополнение нечеткого множества есть единица минус функция принадлежности. Так, если 4 на 0.67 принадлежит множеству около 6, оно также на 0.33 не принадлежит множеству около 6. Закон исключенного третьего был одним из первых среди причин перехода к теории нечетких множеств. В нечетких множествах объект может принадлежать как множеству, так и его дополнению. Это может быть прослежено графически на рис. 15.3.
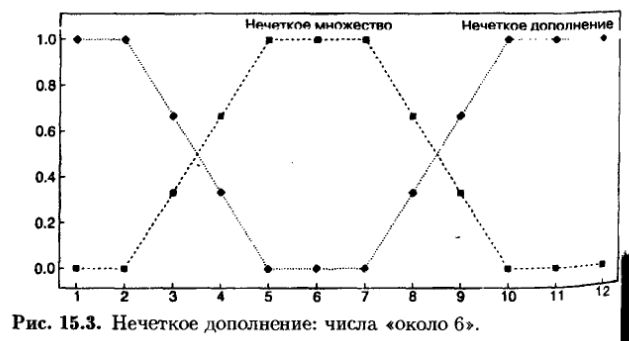
Например, предположим, что некто ростом пять футов одиннадцать дюймов на 0.5 принадлежит множеству высоких людей. При таком определении высоких и не высоких некто пяти футов семи дюймов находится в промежутке – он не высокий и не низкий. Ближе к делу: предположим, что мы оценивали акции и имели множество критериев относительно благоприятной ситуации для покупки. Существует одна акция, которая удовлетворяет всем критериям, кроме одного. Она имеет отношение Р/Е 20, а не 15. С использованием нечетких множеств была бы возможность установить количественную меру, сказав, что эта акция на 0.8 принадлежит множеству «покупать», и это означало бы частичное, но не полное основание для покупки.
Нечеткие множества и вероятность
Теорию нечетких множеств часто путают с теорией вероятностей. В самом деле, ее критики заявляли, что теория нечетких множеств не способна решать задачи, которые не сформулированы в терминах теории вероятностей. Это непонимание является следствием похожести функции принадлежности, которая изменяется от 0 до 1, с вероятностями, которые также изменяются от 0 до 1. За исключением этих величин, две данные меры совершенно различны, хотя обе могут быть описаны как меры неопределенности. Из них каждая измеряет отличный аспект неопределенности.
Нечеткая функция принадлежности является описателем сложного состояния. Дополнительные данные или выборки изменяют этой величины. С другой стороны, вероятности зависят от частоты и случайности. Будущие выборки данных могут изменить вероятность.
Возьмем следующий классический пример нечеткого множества. Предположим, что вы имеете две бутыли с жидкостью. Бутыль А имеет функцию принадлежности 0.9 к множеству питьевых жидкостей, в то время как жидкость в бутыли В имеет 90% вероятности быть питьевой. Если вы вынуждены пить из одной из этих бутылей, то какую вы предпочли бы? Жидкость в бутыли а, в соответствии с ее функцией принадлежности, не совсем питьевая, но похожа на таковую. Это может быть грязная вода. С другой стороны, жидкость в бутыли B имеет 90% вероятности быть полностью питьевой и 10% – быть смертельной. В этом случае жидкость в бутыли В может быть или на 100% питьевой, или на 100% смертельной. Вы не узнаете это, пока не попробуете. Однако, зная, что бутыль А более питьевая, мы бы выбрали именно ее. Заметим, что когда мы пьем из бутыли а, ее функция принадлежности к нечеткому множеству питьевых жидкостей не изменяется. Она остается грязной водой, а величина ее функции принадлежности равной 0.90. Тот факт, что нечеткие множества не зависят от частоты, оказывается важным при рассмотрении поведенческих финансов.
Частичная истина
Нечеткая логика является системой, где дробные величины увеличивают способность теории множеств моделировать реальность. Применение теории нечетких множеств обусловило успехи искусственного интеллекта. В Японии система движения поездов метро основана на нечетких понятиях. Повсюду работающие нечеткие контроллеры, начиная от электробритв до автоматических передач, так же, как и промышленное оборудование, обнаруживают высокую эффективность и приспосабливаемость. В искусственном интеллекте гибриды нечетких правил и нейронных сетей дают в результате системы с высокой способностью к обучению и адаптированию.
В статистическом анализе меньше выразительности, в то время как в области распознавания образов нечеткие множества были применены с большим успехом. Мы увидим далее, что нечеткие множества помогают понять, как люди принимают решения.
Нечеткие множества – это архетип сложных понятий. Для полной принадлежности к нечетному множеству существуют разные критерии, из которых каждый согласован с определением множества. Однако наряду с этим существует неопределенная область, где объекты только частично принадлежат множеству. Чем дальше мы уходим от сердцевины, тем в меньшей степени объект принадлежит множеству или походит на него.
Функция принадлежности не зависит от частоты. Она есть мера состояния и того, насколько объект сравним или походит на идеального члена нечеткого множества, т. е. на такого, у которого функция принадлежности равна 1.0. Эта степень подобия не изменяется при увеличении выборки.?
Мы кратко изучили область, которая кажется точно воспроизводящей количественную сторону того, как большинство людей думают и принимают решения. Интересно то, как мало существует эмпирических исследований, подкрепляющих утверждение Заде и его последователей о том, что люди реально используют нечеткие множества именно таким образом. В другой области – поведенческой психологии – существует много эмпирических данных. Многие из них были связаны с экономикой и рынками.
|